遞推算法👉動態規劃
課程內容#
遞推#
兔子繁殖問題 [引入]#
-

- 題意理解:幼年兔子出生後,過一個月變成成年兔子,再過一個月生下一對幼年兔子 [即第三個月]
- 本月數量 f (n)= 本月成年 + 本月幼年 👇
-

- 本月成年 = 上個月成年 + 上個月幼年 =上個月數量 f (n - 1)
- 本月幼年 = 上個月成年 = 上上個月成年 + 上上個月幼年 =上上個月數量 f (n - 2)[新增兔子數量]
- 👉$f (n) = f (n - 1) + f (n - 2)$< 斐波那契數列 >,f (n) 代表第 n 個月兔子的總數量
-
- 當 n = 60 時,單純用遞歸實現,會出現
- 程序運行效率問題 [重複計算遞推項]
- 解決方法:正向遞推 + 記憶化 [遞歸] 或 逆向遞推 [循環]
- 任何一個遞推問題,都至少有上述 2 種方式實現
- 結果溢出問題 [超過整型表示範圍]
- 程序運行效率問題 [重複計算遞推項]
求解套路⭐#
- ① 確定遞推狀態【⭐⭐⭐】:尋找問題中的自變量和因變量
- 一個數學符號 ➕ 一段對數學符號的描述 [語義信息]
- 確定狀態定義的重點:狀態維度。如何確定?
- 首先確定因變量,再確定相關聯的自變量,得維度
- $f(x) = y$
- y:問題中的求解量,也是我們所謂的因變量
- x:問題中直接影響求解量的部分,也是我們所謂的自變量
- [PS] 看別人題目解答時,重點關注本步驟;[本質]
- ② 推導遞推公式:分析狀態中的容斥關係
- 推導遞推狀態符號的自我表示方法
- 【容斥原理】
-

- 整體面積 = 部分面積相加減
- 👉【相同符號表示下】的公式關係:保持遞推狀態的定義。如兔子問題中:
-

- f (n) 一直是所有兔子的數量,不要偏移到成年或幼年兔子的數量,但可以通過它們來轉換
- $f(n) = f(n - 1) + f(n - 2)$
- $f (n - 1)$,代表第 n - 1 個月的兔子數量 [恰巧等於第 n 個月的成年兔子數量]
- $f (n - 2)$,代表第 n - 2 個月的兔子數量 [恰巧等於第 n 個月的幼年兔子數量]
- 所謂的推導,就是推導上面這兩句話
-
- 推導遞推狀態符號的自我表示方法
- ③ 程序實現[遞歸 + 記憶化 or 循環]
動態規劃#
數字三角形問題 [引入]#
【動態規劃的基本題】HZOJ-43
-

- 記錄每一行每個點可以走出的最大值
- ① 從下往上走
- [首先直接由原值確定最下一行的最大值,通過最大值決策,從下往上依行得到每個點對應的最大值]
- 遞推狀態:$f (i, j)$ 代表從底邊走到點 $(i, j)$ 的最大值
- 遞推公式:$f (i,\ j) = max (f (i+1,\ j),\ f (i+1,\ j+1)) + val (i,\ j)$
- 通過 max【決策】,選擇從左下角 $f (i + 1, j)$ 或右下角 $f (i + 1, j + 1)$ 中的一個狀態【轉移】,該過程又叫狀態轉移過程
- ② 從上往下走
- [與上述過程相反]
- 遞推狀態:f (i, j) 代表從頂點走到點 (i, j) 的最大值
- 遞推公式:$f (i,\ j) = max (f (i-1,\ j),\ f (i-1,\ j-1)) + val (i,\ j)$
- 決策從左上角還是右上角轉移過來
- ❗❗ 從上面兩種方式可以看出,狀態定義極其重要!
- 數字符號完全一致
- 語義信息不同
- 遞歸公式不同
- 【結論】數學符號無法完全代表狀態定義,重點在後面的解釋!
- 🆒 兩種方法的對比
- 本質:狀態定義的對比
- 區別主要在程序實現上
- 第 1 種更優秀
- 不用做邊界判斷;最終結果,直接存儲在 f [0][0] 上
- 第 2 種
- 需要做邊界判斷;最終結果,存儲在一組數據中
- Ⅰ) 邊界判斷,是因為上個狀態可能不存在 👉 可使用補 0 大法
- Ⅱ) 獲取答案,需要遍歷一組數據 / 提前存好
本質理解及求解套路⭐#
動態規劃是遞推問題的一種特殊類型
- 動態規劃:遞推問題中求解最優解的問題
- 類似遞推的套路:①確定遞推狀態⭐⭐⭐、②遞推公式,③證明正確性,④程序實現
-

- 理解第二步:轉移、決策
- 關注所有決定 f (i, j)最優值的狀態 [可轉移的],放入到決策過程中
- 決策,如 max;再轉移
- 勤於第三步:正確性證明 [數學歸納法見下]
- 相比遞推主要多了正確性證明,主要驗證狀態轉移方程的正確性
-
- [可擴展的概念]最優子結構、無後效性、重複子問題等
- [可參考的視頻]數據結構 [國家精品課]- 清華大學:P29~P47——bilibili
+ 數學歸納法#
-

- 可用於證明動態規劃的正確性
- 可用於推導動態規劃的轉移方程
+ 拓撲序#
- 圖形結構是最最抽象的數據結構,必須理解成思維邏輯結構 [神經網絡已經具象化了]
- 引入:在程序中,圖形結構不能用循環來遍歷,而一維序列可以
- 本質:圖形結構 👉 一維序列
- 想像:A 為起床,B、C 分別為穿上、下衣,D、E 分別為刷牙、洗臉,F 為出門
- 則其對應的圖形結構和轉換的拓撲序如下:
-

- 轉換過程:不斷提取入度為 0 的元素 [第一個為 A],並將其從圖中拿掉
- 可見一個固定的圖結構,其拓撲序不唯一
- 👇 所有遞推問題的狀態轉移過程[狀態之間的求解順序],本質上也滿足拓撲序
-

- 參考數字三角形問題
- 必須先知道狀態集合所有元素的值,才能得到最終的決策結果 [存在依賴關係]
-
- [小結]
- 拓撲序是一種圖形結構上的依賴順序,一個圖的拓撲序不唯一
- 掌握拓撲序的話,可以更好地理解遞推問題 [動態規劃]
- 將其理解成一種思維方式!
求解方向#
針對遞推問題 [動態規劃]
- ① 我從哪裡來
- 計算前置的所有狀態,得到當前狀態的結果 [找前面的結點]
- 例如:數字三角形、兔子繁殖、錢幣、牆壁塗色
- [比 “我到哪裡去” 簡單]
- ② 我到哪裡去
- 當前狀態的結果已經正確,要更新後置的所有狀態 [找後面的結點]
- 例如:雜務 [P1113]、神經網絡 [P1038]、旅行計劃 [P1137]
- P:來自洛谷上的題
隨堂練習#
—— 遞推 ——#
爬樓梯#
[HZOJ-40]
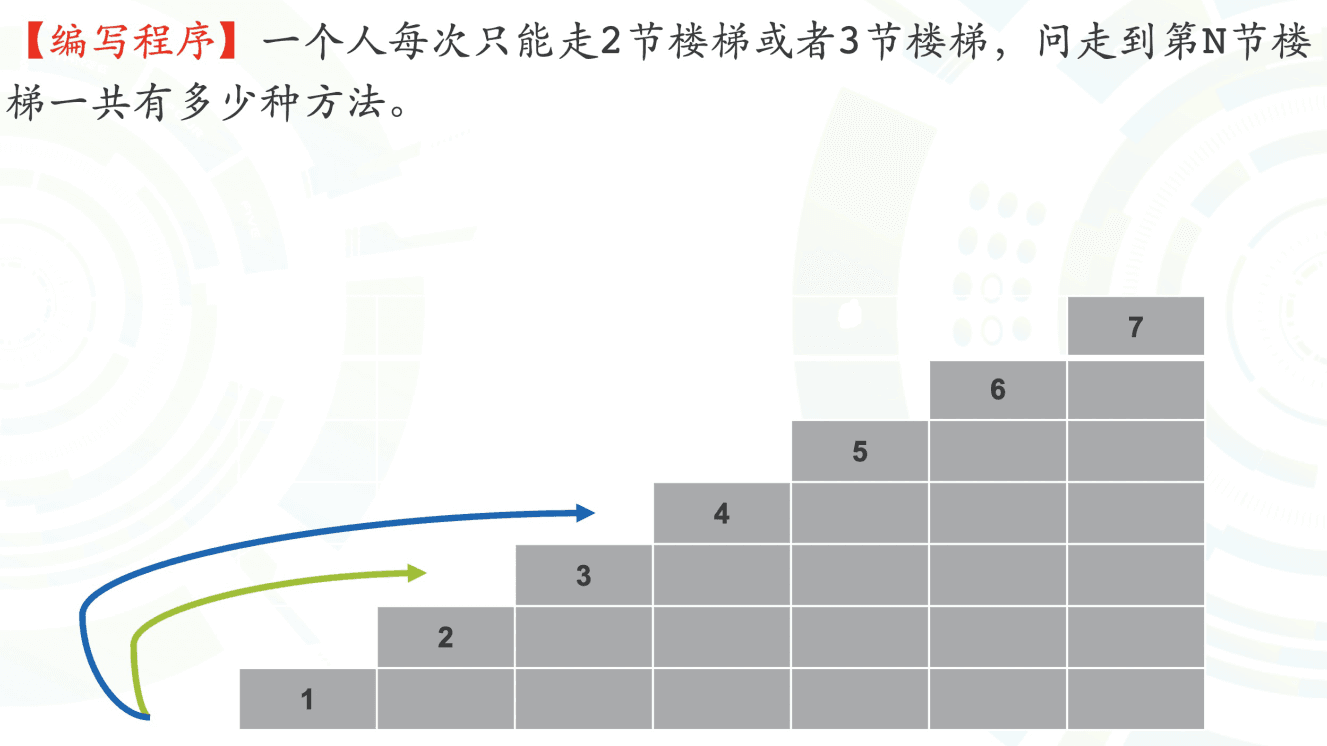
- 確定遞推狀態
- 因變量:方法數
- 自變量:要上的樓梯數
- f (n):上到第 n 節樓梯的方法數
- 推導遞推公式
- 根據最後一步是 2 步還是 3 步劃分 f (n)
- $f(n) = f(n - 2) + f(n - 3)$
錢幣問題#
[HZOJ-42]

- 狀態定義
- 因變量:方法總數
- 自變量:目標金額、使用的錢幣種類
- f (n)(N) :使用前 n 種錢幣,湊得目標金額 N 的方法數
- 遞推公式
- 基於容斥原理:是 / 否使用第 n 種錢幣
- ① 沒用第 n 種錢幣:$f (n - 1)(N)$
- ② 一定用了第 n 種錢幣:$f (n)(N - val (n))$
- val (n):第 n 種錢幣的面額
- 以上關係為等於關係,即數量正好相等;而非準確的表示關係,式子是自己定義的
- [PS] 注意:組合問題,不考慮順序
牆壁塗色#

- 【理解狀態定義的重要性!】狀態不同,遞推公式不同,程序不同
- 難點:環狀,最後一塊顏色與第一塊顏色有關聯
- 3 種方式
- ①關注首尾顏色【通用,需掌握】
- 狀態定義
- 因變量:方案總數
- 自變量:牆壁數量
- ➕ 解題技巧相關的量:頭部顏色、尾部顏色 [需要記錄]
- $f (n, i, j)$:n 塊牆壁,頭部顏色為 i,尾部顏色為 j 的方案總數
- 遞推公式 —— 非環 👉 成環:取出非環的方法中,首尾顏色不一樣的方法
- [先不考慮環]$f (n, i, j) = Σ f (n - 1,\ i,\ k)\ |\ k \neq j$
- 即 n - 1 塊牆壁,頭部顏色為 i,尾部顏色不為 j[相鄰顏色不相同] 的方案總數
- 【再考慮環,得答案】$f (n) = ΣΣ f (n,\ i,\ j)\ |\ i \neq j$
- 即在保證了相鄰顏色不一樣的方案中,首尾顏色不一樣的方案總數
- [先不考慮環]$f (n, i, j) = Σ f (n - 1,\ i,\ k)\ |\ k \neq j$
- 狀態定義
- ②頭部顏色是什麼不重要 [只改變頭部顏色,對應的結果是相等的]
- 狀態定義
- f (n, j):n 塊牆壁,尾部顏色為 j 的方案總數 [頭部顏色默認為 0(隱含條件),假設 3 種顏色的編號為 0、1、2]
- 遞推公式
- [隱含頭部顏色為 0 的條件]$f (n,\ j) = Σf (n - 1,\ k)\ |\ k \neq j$
- 【答案】$f (n) = [f (n, 1) + f (n, 2)] \times 3$👉$f (n, 1) \times 6$
- 6:頭部顏色有 3 種選擇,定了頭部顏色後,尾部顏色有 2 種選擇,即 3 * 2
- 通過實際的計算保證頭尾顏色不一致
- 狀態定義
- ③頭尾顏色都不關注
- 狀態定義 f (n):n 塊牆壁,符合條件 [首尾顏色、相鄰顏色不同] 的方案總數
- 遞推公式
-

- 根據上圖,f (n) 可分為兩種情況:1 和 3 相同、1 和 3 不同 [1 和 4 肯定不同,不好劃分]
- (Ⅰ) 1 和 3 不同:$f (n - 1) \times 1$
- 此時前 n - 1 塊牆壁有合理的塗色,即 f (n - 1) 種方案
- 又 4 號位只剩 1 種顏色選擇,因為 1 和 3 不同,1 和 4 不同,3 和 4 也不同
- (Ⅱ) 1 和 3 相同:$f (n - 2) \times2$
- 1 和 3 相同,1 和 2 必不同,所以此時前 n - 2 塊牆壁有合理的塗色,即 f (n -2) 種方案
- 又 4 號位還剩 2 種顏色選擇,因為 1 和 3 相同,4 只要和 1 不同即可
- (Ⅰ) 1 和 3 不同:$f (n - 1) \times 1$
- 【答案】$f (n) = f (n - 2) \times 2 + f (n - 1)$,等式僅在 n ≥ 4 時成立
- [延伸] 如果顏色種數為 k,$f (n) = f (n - 2) \times (k -1) + f (n - 1) \times (k - 2)$
-
- [PS] 太巧妙,需要靈性
- ①關注首尾顏色【通用,需掌握】
HZOJ-41:牆壁塗色#


樣例輸入
5 3
樣例輸出
30
- 思路
- 相比上題,區別在於顏色種數為 k,而不是 3
- 使用上述第 3 種方式:$f (n) = f (n - 2) \times (k -1) + f (n - 1) \times (k - 2)\ [n ≥ 4]$
- 【注意】根據數據規模,方案總數可能變成大整數,需利用數據結構
- 代碼
-

- 【算法】利用循環,以及三個數 [需要記錄 3 項狀態 f] 來回倒,先推算出 f (1)、f (2)、f (3) 的值
- f (1)、f (2)、f (3) 不滿足通用公式 [n ≥ 4]
- f (3) 的值存在 f [0] 中
- 模 3 的使用,讓數組滾動起來
- 【數據結構】對於大整數情況,只需更換數據構造 int→BigInt
-
—— 動態規劃 ——#
HZOJ-44:最長上升子序列#

樣例輸入
10
3 2 5 7 4 5 7 9 6 8
樣例輸出
5
- 思路
- 普通版
- 能夠挑出來的最長嚴格上升子序列[不需要連續挑]
- 狀態定義
- $dp (i)$:代表以索引為 $i$ 的元素結尾的最長嚴格上升序列長度
- 必須以 $i$ 結尾!
- 狀態轉移
- $dp(i) = max{dp(j)} + 1\ |\ j<i,\ val(j) < val(i)$
- 所有能夠轉移到 $dp (i)$ 的狀態:滿足 $j<i,\ val (j)<val (i)$ 條件的 $f (j)$,共 $i$ 個
- 決策:$max$
- 最終答案:$max (f (i))$,在所有的 $dp (i)$ 中取最大值
- 狀態轉移的時間複雜度:$O (n^2)$
- 優化版 —— 轉移過程
- 普通版
- 代碼
- 普通版

- 數據很大,使用 scanf,而不是 cin
- 注意兩個 max 的含義
- 狀態轉移的時間效率低
- 普通版
HZOJ-45:最長公共子序列#

樣例輸入
sehuaizexi
yhaizeyiux
樣例輸出
6
- 思路
- 狀態定義
- $dp (i,\ j)$:代表第 1 個字符串取前 i 位,第 2 個字符串取前 j 位,對應的最長公共子序列的長度
- 狀態轉移
- $dp(i) = \left{\begin{aligned}&max{dp(i-1,\ j),\ dp(i,\ j-1)} &s1(i)\neq s2(j)\&dp(i-1,\ j-1)+1&s1(i)=s2(j)\end{aligned}\right.$
- ⭐參與決策的狀態數量,是會根據條件不同而改變的
- 取決於【字符串 1 的第 i 位】和【字符串 2 的第 j 位】是否相等
- 待決策的狀態數量為 2 個或 1 個,上一題的數量為 i 個
- [PS]
- 情況 2 不需要決策,其值一定不小於情況 1,因為情況 1 中 $dp (i-1,\ j)$ 或 $f (i,\ j-1)$ 最多比情況 2 中 $f (i-1,\ j-1)$ 大 1
- 但情況 2 加入情況 1 的決策肯定沒錯,即在情況 2 下,$dp (i)=max {dp (i-1,\ j),\ dp (i,\ j-1),\ dp (i-1,\ j-1)+1}$
- 狀態轉移的時間複雜度:$O (n \times m)$
- 狀態定義
- 代碼

- 簡化版:可以少一行代碼,情況 2 的值肯定不小於情況 1
- 注意:dp 從 dp [1][1] 開始,但字符串索引從 0 開始
Tips#
- 要把一道題做成一類題
- vim 下快速複製整行 ——shift + v——visual line 模式
- 有些現象我們可以不理解,但不要輕易去否定,因為最聰明的人不是我們,存在即合理

