1 再帰から動的計画法へ（上）

再帰アルゴリズム👉動的計画法

コース内容#

再帰#

ウサギの繁殖問題 [導入]#

問題の理解：幼いウサギは生まれてから 1 か月後に成長したウサギになり、さらに 1 か月後に幼いウサギのペアを生む [つまり 3 か月目]
今月の数 f (n)= 今月の成長したウサギ + 今月の幼いウサギ 👇
- 今月の成長したウサギ = 先月の成長したウサギ + 先月の幼いウサギ =先月の数 f (n - 1)
- 今月の幼いウサギ = 先月の成長したウサギ = 先々月の成長したウサギ + 先々月の幼いウサギ =先々月の数 f (n - 2)[新たなウサギの数]
- 👉$f (n) = f (n - 1) + f (n - 2)$< フィボナッチ数列 >、f (n) は n か月目のウサギの総数を表す
n = 60 のとき、単純に再帰を使うと、次の問題が発生する
- プログラムの実行効率の問題 [再帰項の重複計算]
  - 解決方法：前向き再帰 + メモ化 [再帰] または後向き再帰 [ループ]
  - どんな再帰問題でも、少なくとも上記の 2 つの方法で実現できる
- 結果のオーバーフローの問題 [整数の表現範囲を超える]

解法のパターン⭐#

① 再帰状態を特定する【⭐⭐⭐】：問題の自変数と因変数を探す
- 数学記号 ➕ 数学記号の説明の一部 [意味情報]
- 状態定義のポイントを特定する：状態の次元。どうやって特定する？
  - まず因変数を特定し、次に関連する自変数を特定して次元を得る
  - $f(x) = y$
  - y：問題の解決量、つまり我々が言う因変数
  - x：問題の解決量に直接影響を与える部分、つまり我々が言う自変数
- [PS] 他の人の問題解答を見るときは、このステップに重点を置く；[本質]
② 再帰公式を導出する：状態の包含排除関係を分析する
- 再帰状態記号の自己表現方法を導出する
  - 【包含排除原理】
  - 全体の面積 = 部分の面積の合計と差
- 👉【同じ記号表示下】の公式関係：再帰状態の定義を保持する。ウサギの問題では：
  - f (n) は常にすべてのウサギの数であり、成長したウサギや幼いウサギの数に偏らないが、それらを通じて変換することができる
    - $f(n) = f(n - 1) + f(n - 2)$
    - $f (n - 1)$ は n - 1 か月目のウサギの数を表す [ちょうどn か月目の成長したウサギの数に等しい]
    - $f (n - 2)$ は n - 2 か月目のウサギの数を表す [ちょうどn か月目の幼いウサギの数に等しい]
    - いわゆる導出とは、上記の 2 つの文を導出すること
③ プログラムの実装[再帰 + メモ化 or ループ]

動的計画法#

数字三角形問題 [導入]#

【動的計画法の基本問題】HZOJ-43

各行の各点から出る最大値を記録する
① 下から上へ移動する
- [まず元の値から最下行の最大値を決定し、最大値からの決定で下から上に各点の最大値を得る]
- 再帰状態：$f (i, j)$ は底辺から点 $(i, j)$ までの最大値を表す
- 再帰公式：$f (i,\ j) = max (f (i+1,\ j),\ f (i+1,\ j+1)) + val (i,\ j)$
  - max【決定】を通じて、左下の $f (i + 1, j)$ または右下の $f (i + 1, j + 1)$ のいずれかの状態を選択する【遷移】、このプロセスは状態遷移プロセスとも呼ばれる
② 上から下へ移動する
- [上記のプロセスとは逆]
- 再帰状態：f (i, j) は頂点から点 (i, j) までの最大値を表す
- 再帰公式：$f (i,\ j) = max (f (i-1,\ j),\ f (i-1,\ j-1)) + val (i,\ j)$
  - 左上角または右上角からの遷移を決定する
❗❗ 上記の 2 つの方法から、状態定義が非常に重要であることがわかる！
- 数字記号は完全に一致
- 意味情報は異なる
- 再帰公式は異なる
- 【結論】数学記号は状態定義を完全に表すことができず、重要なのは後の説明である！
🆒 2 つの方法の比較
- 本質：状態定義の比較
- 主な違いはプログラムの実装にある
- 第 1 の方法が優れている
  - 境界判断を行う必要がない；最終結果は直接 f [0][0] に保存される
- 第 2 の方法
  - 境界判断が必要；最終結果は一組のデータに保存される
  - Ⅰ) 境界判断は、前の状態が存在しない可能性があるため 👉 0 を補う方法
  - Ⅱ) 答えを得るには、一組のデータを遍歴する必要がある / 事前に保存する

本質的理解と解法のパターン⭐#

動的計画法は再帰問題の特別なタイプである

動的計画法：再帰問題の中で最適解を求める問題
再帰のパターンに似た：①再帰状態を特定する⭐⭐⭐、②再帰公式、③正当性の証明、④プログラムの実装
- 第二ステップの理解：遷移、決定
  - すべての決定 f (i, j)最適値の状態 [遷移可能な] に注目し、決定プロセスに入れる
  - 決定、例えば max；その後遷移
- 第三ステップに勤勉であること：正当性の証明 [数学的帰納法は下記参照]
- 再帰に比べて主に正当性の証明が追加され、状態遷移方程式の正当性を検証することが主な目的である
[拡張可能な概念]最適部分構造、無後効果性、重複部分問題など
[参考動画]データ構造 [国家精品課]- 清華大学：P29~P47——bilibili

+ 数学的帰納法#

動的計画法の正当性を証明するために使用できる
動的計画法の遷移方程式を導出するために使用できる

+ トポロジカル順序#

グラフィック構造は最も抽象的なデータ構造であり、思考論理構造として理解する必要がある [神経ネットワークはすでに具象化されている]
導入：プログラム内では、グラフィック構造をループで遍歴することはできず、一次元系列は可能である
本質：グラフィック構造 👉 一次元系列
想像：A は起床、B、C はそれぞれ服を着る、D、E はそれぞれ歯を磨く、顔を洗う、F は出かける
- その場合、対応するグラフィック構造と変換のトポロジカル順序は次のようになります：
- 変換プロセス：入次数が 0 の要素を繰り返し抽出し [最初は A]、それをグラフから取り除く
- 固定のグラフ構造があり、そのトポロジカル順序は一意ではないことがわかる
👇 すべての再帰問題の状態遷移プロセス[状態間の解決順序] も本質的にトポロジカル順序を満たす
- 数字三角形問題を参照
- 状態集合のすべての要素の値を最初に知る必要があり、最終的な決定結果を得ることができる [依存関係が存在する]
[小結]
- トポロジカル順序はグラフィック構造上の依存順序であり、グラフのトポロジカル順序は一意ではない
- トポロジカル順序を理解すれば、再帰問題 [動的計画法] をよりよく理解できる
- それを思考方法として理解すること！

解決方向#

再帰問題に対して [動的計画法]

① どこから来たのか
- 前置のすべての状態を計算し、現在の状態の結果を得る [前のノードを探す]
- 例：数字三角形、ウサギの繁殖、コイン、壁の塗装
- [「どこに行くのか」より簡単]
② どこに行くのか
- 現在の状態の結果はすでに正しいので、後置のすべての状態を更新する必要がある [後のノードを探す]
- 例：雑務 [P1113]、神経ネットワーク [P1038]、旅行計画 [P1137]
- P：洛谷の問題から

授業中の練習#

—— 再帰 ——#

階段を登る#

[HZOJ-40]

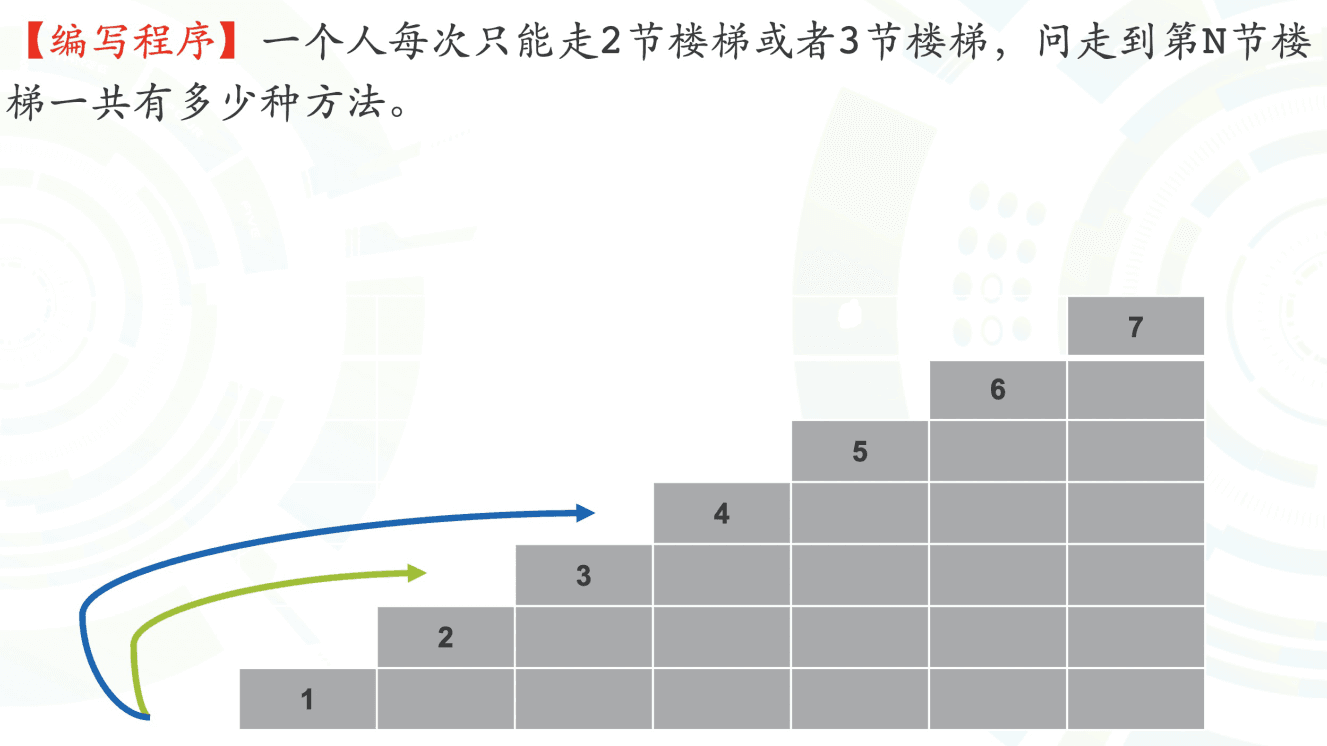
再帰状態を特定する
- 因変数：方法の数
- 自変数：登る階段の数
- f (n)：n 段目の階段に上る方法の数
再帰公式を導出する
- 最後のステップが 2 ステップか 3 ステップかで f (n) を区分する
- $f(n) = f(n - 2) + f(n - 3)$

コイン問題#

[HZOJ-42]

状態定義
- 因変数：方法の総数
- 自変数：目標金額、使用するコインの種類
- f (n)(N) ：前 n 種類のコインを使用して目標金額 N を得る方法の数
再帰公式
- 包含排除原理に基づく：第 n 種類のコインを使用するかどうか
- ① 第 n 種類のコインを使用しない：$f (n - 1)(N)$
- ② 第 n 種類のコインを必ず使用する：$f (n)(N - val (n))$
  - val (n)：第 n 種類のコインの額面
  - 上記の関係は等式関係であり、数量がちょうど等しいことを示す；正確な表示関係ではなく、式は自分で定義したものである
[PS] 注意：組み合わせ問題では、順序を考慮しない

壁の塗装#

【状態定義の重要性を理解する！】状態が異なれば、再帰公式が異なり、プログラムも異なる
難点：環状で、最後の色が最初の色に関連している
3 つの方法
- ① 首尾の色に注目【一般的で、習得が必要】
  - 状態定義
    - 因変数：方案の総数
    - 自変数：壁の数
      - ➕ 解法に関連する量：頭部の色、尾部の色 [記録が必要]
    - $f (n, i, j)$：n 枚の壁、頭部の色が i、尾部の色が j の方案の総数
  - 再帰公式 —— 非環 👉 環：非環の方法の中で、首尾の色が異なる方法を取る
    - [まず環を考慮しない]$f (n, i, j) = Σ f (n - 1,\ i,\ k)\ |\ k \neq j$
      - つまり n - 1 枚の壁、頭部の色が i、尾部の色が j でない[隣接色が異なる] の方案の総数
    - 【環を考慮すると、答えを得る】$f (n) = ΣΣ f (n,\ i,\ j)\ |\ i \neq j$
      - つまり隣接色が異なる方案の中で、首尾の色が異なる方案の総数
- ② 頭部の色が何であるかは重要でない [頭部の色を変えるだけで、対応する結果は等しい]
  - 状態定義
    - f (n, j)：n 枚の壁、尾部の色が j の方案の総数 [頭部の色は 0（暗黙の条件）と仮定し、3 色の番号は 0、1、2]
  - 再帰公式
    - [暗黙の頭部の色が 0 の条件]$f (n,\ j) = Σf (n - 1,\ k)\ |\ k \neq j$
    - 【答え】$f (n) = [f (n, 1) + f (n, 2)] \times 3$👉$f (n, 1) \times 6$
      - 6：頭部の色には 3 つの選択肢があり、頭部の色を決めた後、尾部の色には 2 つの選択肢がある、つまり 3 * 2
      - 実際の計算を通じて頭尾の色が一致しないことを保証する
- ③ 頭尾の色を気にしない
  - 状態定義 f (n)：n 枚の壁、条件を満たす [首尾の色、隣接色が異なる] の方案の総数
  - 再帰公式
    - 上の図に基づき、f (n) は2 つの場合に分けられる：1 と 3 が同じ、1 と 3 が異なる [1 と 4 は必ず異なるので、分けるのが難しい]
      - (Ⅰ) 1 と 3 が異なる：$f (n - 1) \times 1$
        
        この時、前 n - 1 枚の壁には合理的な塗装があり、つまり f (n - 1) 種の方案
        
        さらに 4 号位置には 1 つの色の選択肢しか残っていない、なぜなら 1 と 3 が異なり、1 と 4 も異なり、3 と 4 も異なるから
      - (Ⅱ) 1 と 3 が同じ：$f (n - 2) \times2$
        
        1 と 3 が同じであれば、1 と 2 は必ず異なるので、この時前 n - 2 枚の壁には合理的な塗装があり、つまり f (n -2) 種の方案
        
        さらに 4 号位置には 2 つの色の選択肢が残っている、なぜなら 1 と 3 が同じであれば、4 は 1 と異なるだけでよい
    - 【答え】$f (n) = f (n - 2) \times 2 + f (n - 1)$、等式は n ≥ 4 のときのみ成立
    - [延伸] 色の種類が k の場合、$f (n) = f (n - 2) \times (k -1) + f (n - 1) \times (k - 2)$
  - [PS] 非常に巧妙で、直感が必要

HZOJ-41：壁の塗装#

サンプル入力

5 3

サンプル出力

思考
- 前の問題と比較して、色の種類が k である点が異なる
- 上記の第 3 の方法を使用：$f (n) = f (n - 2) \times (k -1) + f (n - 1) \times (k - 2)\ [n ≥ 4]$
- 【注意】データ規模に応じて、方案の総数が大きな整数になる可能性があるため、データ構造を利用する必要がある
コード
- 【アルゴリズム】ループを利用し、3 つの数 [3 項目の状態 f を記録する必要がある] を行き来して、まず f (1)、f (2)、f (3) の値を推算する
  - f (1)、f (2)、f (3) は一般的な公式を満たさない [n ≥ 4]
  - f (3) の値は f [0] に存在する
  - mod3 の使用により、配列をロールさせる
- 【データ構造】大きな整数の場合は、データ構造を int→BigInt に変更するだけでよい
  - f [3] 配列の型を int から BigInt に変更し、BigInt 型を作成し、cout をオーバーロードするだけでよい
  - C++ の知識 [オーバーロード、参照など] に関するものであり、本節の重点ではない
  - 大きな整数の加算、大きな整数の乗算の考え方については、大きな整数加法、大きな整数乗法を参照
  - [PS] プログラム = アルゴリズム (効率) + データ構造 (表現能力)

—— 動的計画法 ——#

HZOJ-44：最長上昇部分列#

サンプル入力

10
3 2 5 7 4 5 7 9 6 8

サンプル出力

思考
- 通常版
  - 選び出せる最長の厳密上昇部分列[連続して選ぶ必要はない]
  - 状態定義
    - $dp (i)$：インデックス $i$ の要素で終わる最長厳密上昇列の長さを表す
    - 必ず$i$ で終わる！
  - 状態遷移
    - $dp(i) = max{dp(j)} + 1\ |\ j<i,\ val(j) < val(i)$
    - $dp (i)$ に遷移できるすべての状態：$j<i,\ val (j)<val (i)$ の条件を満たす $f (j)$、合計 $i$ 個
    - 決定：$max$
  - 最終的な答え：$max (f (i))$、すべての $dp (i)$ の中から最大値を取る
  - 状態遷移の時間計算量：$O (n^2)$
- 最適版 —— 遷移プロセス
  - 次に進む：2 再帰から動的計画法（下）
コード
- 通常版
  - データが大きいため、scanf を使用し、cin ではなく
  - 2 つの max の意味に注意
  - 状態遷移の時間効率が低い

HZOJ-45：最長共通部分列#

サンプル入力

sehuaizexi
yhaizeyiux

サンプル出力

思考
- 状態定義
  - $dp (i,\ j)$：第 1 の文字列の最初の i 文字、第 2 の文字列の最初の j 文字に対応する最長共通部分列の長さを表す
- 状態遷移
  - $dp(i) = \left{\begin{aligned}&max{dp(i-1,\ j),\ dp(i,\ j-1)} &s1(i)\neq s2(j)\&dp(i-1,\ j-1)+1&s1(i)=s2(j)\end{aligned}\right.$
  - ⭐決定に参加する状態の数は、条件によって異なる
    - 【文字列 1 の第 i 文字】と【文字列 2 の第 j 文字】が等しいかどうかに依存する
    - 決定待ちの状態の数は 2 または 1 であり、前の問題の数は i 個
    - [PS]
      - 状況 2 では決定が必要なく、その値は状況 1 より小さくなることはない、なぜなら状況 1 の中の $dp (i-1,\ j)$ または $f (i,\ j-1)$ は状況 2 の中の $f (i-1,\ j-1)$ よりも大きくて 1 である可能性があるから
      - しかし状況 2 に状況 1 の決定を追加することは間違いなくない、つまり状況 2 の下で $dp (i)=max {dp (i-1,\ j),\ dp (i,\ j-1),\ dp (i-1,\ j-1)+1}$ である
  - 状態遷移の時間計算量：$O (n \times m)$
コード
- 簡略版：1 行のコードを減らすことができ、状況 2 の値は状況 1 より小さくなることはない
- 注意：dp は dp [1][1] から始まるが、文字列のインデックスは 0 から始まる

ヒント#

問題を 1 つのタイプにまとめる
vim で素早く行全体をコピーする ——shift + v——visual line モード
我々が理解できない現象もあるが、軽々しく否定しないでください、なぜなら最も賢い人は我々ではなく、存在することは合理的である