Recursion Algorithm 👉 Dynamic Programming
Course Content#
Recursion#
Rabbit Breeding Problem [Introduction]#
-

- Understanding the problem: Young rabbits become adult rabbits after one month, and then give birth to a pair of young rabbits after another month [i.e., the third month]
- This month's quantity f(n) = Adult this month + Young this month 👇
-

- Adults this month = Adults last month + Young last month = Last month's quantity f(n - 1)
- Young this month = Adults last month = Adults two months ago + Young two months ago = Two months ago's quantity f(n - 2) [New rabbits]
- 👉$f(n) = f(n - 1) + f(n - 2)$ , f(n) represents the total number of rabbits in the nth month
-
- When n = 60, simply using recursion will result in
- Program efficiency issues [Repeated calculations of recursive terms]
- Solution: Forward recursion + Memoization [Recursion] or Backward recursion [Loop]
- Any recursive problem can be implemented in at least the above two ways
- Result overflow issues [Exceeding integer representation range]
- Program efficiency issues [Repeated calculations of recursive terms]
Solving Routine ⭐#
- ① Determine the recursive state【⭐⭐⭐】: Identify the independent and dependent variables in the problem
- A mathematical symbol ➕ A description of the mathematical symbol [Semantic information]
- Key point in determining state definition: State dimensions. How to determine?
- First determine the dependent variable, then determine the associated independent variables to get the dimensions
- $f(x) = y$
- y: The solving quantity in the problem, also known as the dependent variable
- x: The part in the problem that directly affects the solving quantity, also known as the independent variable
- [PS] When looking at others' problem solutions, focus on this step; [Essence]
- ② Derive the recursive formula: Analyze the inclusion-exclusion relationship in the state
- Derive a self-representing method for the recursive state symbol
- 【Inclusion-Exclusion Principle】
-

- Total area = Sum of partial areas
- 👉 Formula relationship under the same symbol representation: Maintain the definition of the recursive state. For the rabbit problem:
-

- f(n) is always the total number of rabbits, do not shift to the number of adult or young rabbits, but can convert through them
- $f(n) = f(n - 1) + f(n - 2)$
- $f(n - 1)$ represents the number of rabbits in the n - 1 month [coincidentally equal to the number of adult rabbits in the nth month]
- $f(n - 2)$ represents the number of rabbits in the n - 2 month [coincidentally equal to the number of young rabbits in the nth month]
- The so-called derivation is to derive the above two statements
-
- Derive a self-representing method for the recursive state symbol
- ③ Program Implementation [Recursion + Memoization or Loop]
Dynamic Programming#
Number Triangle Problem [Introduction]#
【Basic problem of dynamic programming】HZOJ-43
-

- Record the maximum value that can be reached from each point in each row
- ① Move from bottom to top
- [First directly determine the maximum value of the bottom row from the original values, and then use the maximum value to decide the maximum value corresponding to each point row by row from bottom to top]
- Recursive state: $f(i, j)$ represents the maximum value from the bottom edge to the point $(i, j)$
- Recursive formula: $f(i,\ j) = max(f(i+1,\ j),\ f(i+1,\ j+1)) + val(i,\ j)$
- By max【decision-making】, choose one state from the lower left $f(i + 1, j)$ or the lower right $f(i + 1, j + 1)$【transfer process】, this process is also called state transfer process
- ② Move from top to bottom
- [Opposite to the above process]
- Recursive state: f(i, j) represents the maximum value from the vertex to the point (i, j)
- Recursive formula: $f(i,\ j) = max(f(i-1,\ j),\ f(i-1,\ j-1)) + val(i,\ j)$
- Decision to transfer from the upper left or upper right
- ❗❗ From the above two methods, it can be seen that state definition is extremely important!
- Numerical symbols are completely consistent
- Semantic information is different
- Recursive formulas are different
- 【Conclusion】 Mathematical symbols cannot fully represent state definitions, the focus is on the subsequent explanations!
- 🆒 Comparison of the two methods
- Essence: Comparison of state definitions
- The main difference lies in program implementation
- The first method is superior
- No need for boundary checks; the final result is directly stored in f[0][0]
- The second method
- Requires boundary checks; the final result is stored in a set of data
- Ⅰ) Boundary checks are necessary because the previous state may not exist 👉 Can use Padding with Zero Method
- Ⅱ) To get the answer, it is necessary to traverse a set of data / store it in advance
Essential Understanding and Solving Routine ⭐#
Dynamic programming is a special type of recursive problem
- Dynamic programming: The problem of finding the optimal solution in recursive problems
- Similar recursive routine: ① Determine the recursive state ⭐⭐⭐, ② Recursive formula, ③ Prove correctness, ④ Program implementation
-

- Understand the second step: Transfer, Decision-making
- Focus on all states that determine the optimal value of f(i, j) [transferable], and include them in the decision-making process
- Decision-making, such as max; then transfer
- Be diligent in the third step: Proof of correctness [Mathematical induction see below]
- Compared to recursion, it mainly adds a proof of correctness, mainly verifying the correctness of the state transfer equation
-
- [Expandable concepts]Optimal substructure, No aftereffect, Repeated subproblems etc.
- [Refer to the video]Data Structures [National Quality Course] - Tsinghua University: P29~P47——bilibili
+ Mathematical Induction#
-

- Can be used to prove the correctness of dynamic programming
- Can be used to derive the transfer equation of dynamic programming
+ Topological Order#
- Graph structures are the most abstract data structures and must be understood as logical structures [Neural networks have already visualized it]
- Introduction: In programs, graph structures cannot be traversed using loops, while one-dimensional sequences can
- Essence: Graph structure 👉 One-dimensional sequence
- Imagine: A is getting up, B and C are putting on and taking off clothes, D and E are brushing teeth and washing face, F is going out
- The corresponding graph structure and the converted topological order are as follows:
-

- Conversion process: Continuously extract elements with an in-degree of 0 [the first is A] and remove them from the graph
- It can be seen that a fixed graph structure has a non-unique topological order
- 👇 The state transfer process of all recursive problems [the order of solving between states] essentially also satisfies the topological order
-

- Refer to the number triangle problem
- It is necessary to know the values of all elements in the state set before obtaining the final decision result [there is a dependency relationship]
-
- [Summary]
- Topological order is a dependency order in a graph structure, and a graph's topological order is not unique
- Mastering topological order can help better understand recursive problems [dynamic programming]
- Understand it as a way of thinking!
Solving Direction#
For recursive problems [dynamic programming]
- ① Where do I come from
- Calculate all preceding states to obtain the result of the current state [find the previous nodes]
- For example: Number triangle, Rabbit breeding, Coin, Wall painting
- [Easier than "Where am I going"]
- ② Where am I going
- The result of the current state is already correct, and it is necessary to update all subsequent states [find the following nodes]
- For example: Miscellaneous [P1113], Neural network [P1038], Travel plan [P1137]
- P: From Luogu problems
In-Class Exercises#
——Recursion——#
Climbing Stairs#
[HZOJ-40]
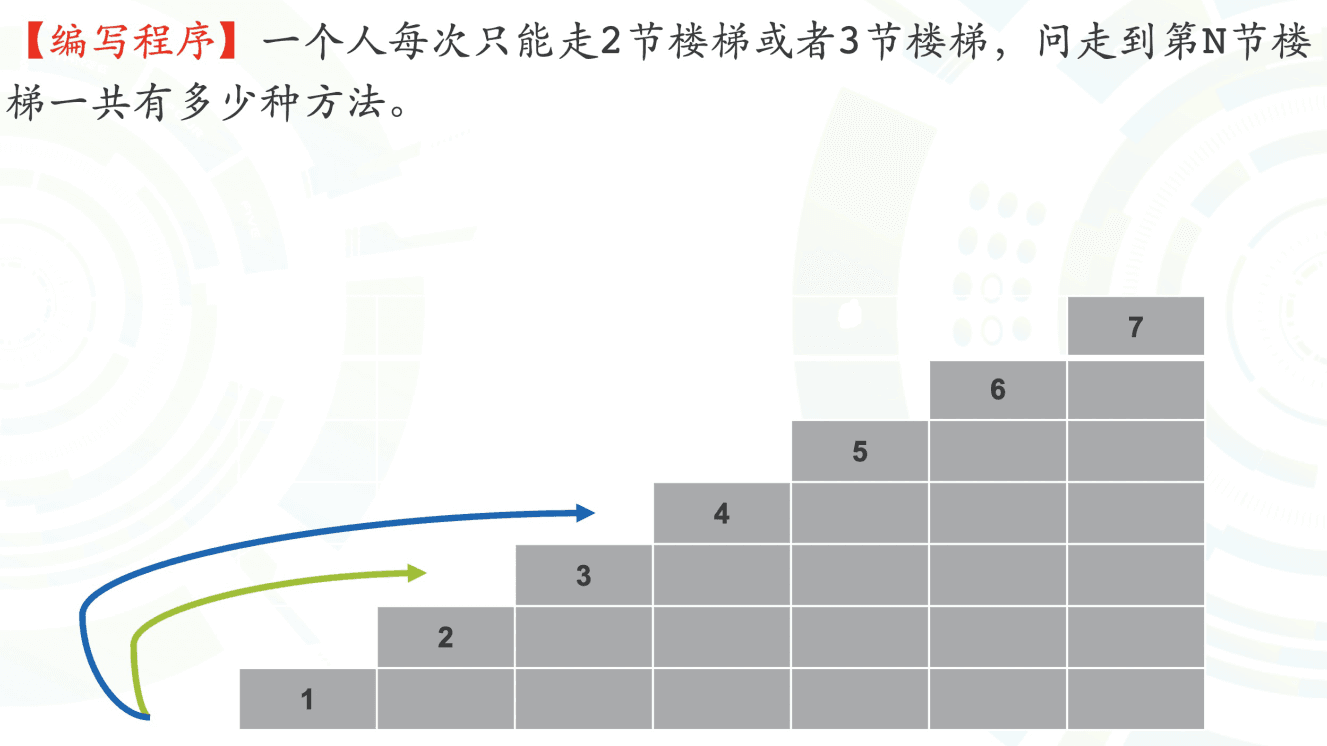
- Determine the recursive state
- Dependent variable: Number of methods
- Independent variable: Number of stairs to climb
- f(n): Number of methods to reach the nth step
- Derive the recursive formula
- Divide f(n) based on whether the last step is 2 steps or 3 steps
- $f(n) = f(n - 2) + f(n - 3)$
Coin Problem#
[HZOJ-42]

- State definition
- Dependent variable: Total number of methods
- Independent variable: Target amount, types of coins used
- f(n)(N): Number of methods to make the target amount N using the first n types of coins
- Recursive formula
- Based on the inclusion-exclusion principle: whether to use the nth type of coin
- ① Not using the nth type of coin: $f(n - 1)(N)$
- ② Definitely using the nth type of coin: $f(n)(N - val(n))$
- val(n): The denomination of the nth type of coin
- The above relationship is an equality relationship, meaning the quantities are exactly equal; not an accurate representation relationship, the formula is self-defined
- [PS] Note: In combination problems, order does not matter
Wall Painting#

- 【Understanding the importance of state definition!】 Different states lead to different recursive formulas and programs
- Difficulty: Circular, the last color is related to the first color
- 3 methods
- ① Focus on the colors at the ends [General, need to master]
- State definition
- Dependent variable: Total number of schemes
- Independent variable: Number of walls
- ➕ Related quantities for solving the problem: Head color, Tail color [Need to record]
- $f(n, i, j)$: Total number of schemes for n walls, head color i, tail color j
- Recursive formula — Non-circular 👉 Circular: Take out the methods in non-circular where head and tail colors are different
- [Do not consider the circle first] $f(n, i, j) = Σ f(n - 1,\ i,\ k)\ |\ k \neq j$
- That is, the total number of schemes for n - 1 walls, head color i, tail color not j [Adjacent colors are different]
- 【Then consider the circle, get the answer】$f(n) = ΣΣ f(n,\ i,\ j)\ |\ i \neq j$
- That is, in the schemes where adjacent colors are different, the total number of schemes where head and tail colors are different
- [Do not consider the circle first] $f(n, i, j) = Σ f(n - 1,\ i,\ k)\ |\ k \neq j$
- State definition
- ② The head color does not matter [Only changing the head color results in equal outcomes]
- State definition
- f(n, j): Total number of schemes for n walls, tail color j [Head color is implicitly 0 (implicit condition), assuming 3 colors are numbered 0, 1, 2]
- Recursive formula
- [Implicit condition of head color being 0] $f(n,\ j) = Σf(n - 1,\ k)\ |\ k \neq j$
- 【Answer】$f(n) = [f(n, 1) + f(n, 2)] \times 3$ 👉 $f(n, 1) \times 6$
- 6: There are 3 choices for the head color, after determining the head color, there are 2 choices for the tail color, i.e., 3 * 2
- Ensure that the head and tail colors are different through actual calculations
- State definition
- ③ Not focusing on either head or tail color
- State definition f(n): Total number of schemes that meet the conditions [head and tail colors, adjacent colors different]
- Recursive formula
-

- According to the above figure, f(n) can be divided into two cases: 1 and 3 are the same, 1 and 3 are different [1 and 4 must be different, difficult to divide]
- (Ⅰ) 1 and 3 are different: $f(n - 1) \times 1$
- At this time, the previous n - 1 walls have reasonable coloring, i.e., f(n - 1) schemes
- The 4th position has only 1 color choice left because 1 and 3 are different, 1 and 4 are different, and 3 and 4 are also different
- (Ⅱ) 1 and 3 are the same: $f(n - 2) \times 2$
- 1 and 3 are the same, so 1 and 2 must be different, thus the previous n - 2 walls have reasonable coloring, i.e., f(n - 2) schemes
- The 4th position still has 2 color choices left because 1 and 3 are the same, and the 4th only needs to be different from 1
- (Ⅰ) 1 and 3 are different: $f(n - 1) \times 1$
- 【Answer】$f(n) = f(n - 2) \times 2 + f(n - 1)$, the equation only holds when n ≥ 4
- [Extension] If the number of colors is k, $f(n) = f(n - 2) \times (k -1) + f(n - 1) \times (k - 2)$
-
- [PS] Very clever, requires intuition
- ① Focus on the colors at the ends [General, need to master]
HZOJ-41: Wall Painting#


Sample Input
5 3
Sample Output
30
- Thought
- Compared to the previous problem, the difference is that the number of colors is k, not 3
- Use the above third method: $f(n) = f(n - 2) \times (k -1) + f(n - 1) \times (k - 2)\ [n ≥ 4]$
- 【Note】 Depending on the data scale, the total number of schemes may become a large integer, requiring the use of data structures
- Code
-

- 【Algorithm】 Use loops and three numbers [need to record 3 states f] to roll back and forth, first calculate the values of f(1), f(2), and f(3)
- f(1), f(2), and f(3) do not satisfy the general formula [n ≥ 4]
- The value of f(3) is in f[0]
- Using mod 3 allows the array to roll
- 【Data Structure】 For large integer situations, just change the data structure from int to BigInt
- Change the type of f[3] array from int to BigInt, then create BigInt type and overload cout
-

-

- Involves C++ knowledge [overloading, references, etc.], which is not the focus of this section
- Involves large integer addition and multiplication of large integers, refer to "Interview and Written Algorithm"——Large Integer Addition、Large Integer Multiplication
- [PS] Program = Algorithm (Efficiency) + Data Structure (Representation Ability)
-
——Dynamic Programming——#
HZOJ-44: Longest Increasing Subsequence#

Sample Input
10
3 2 5 7 4 5 7 9 6 8
Sample Output
5
- Thought
- Ordinary version
- The longest strictly increasing subsequence that can be selected [does not need to be continuous]
- State definition
- $dp(i)$: Represents the length of the longest strictly increasing subsequence ending with the element at index $i$
- Must end with $i$!
- State transfer
- $dp(i) = max{dp(j)} + 1\ |\ j<i,\ val(j) < val(i)$
- All states that can transfer to $dp(i)$: those satisfying $j<i,\ val(j)<val(i)$ condition, a total of $i$ states
- Decision: $max$
- Final answer: $max(f(i))$, take the maximum value among all $dp(i)$
- Time complexity of state transfer: $O(n^2)$
- Optimized version — Transfer process
- Transition to: 2 From Recursion to Dynamic Programming (Part 2)
- Ordinary version
- Code
- Ordinary version

- Data is large, use scanf instead of cin
- Note the meaning of the two max
- Time efficiency of state transfer is low
- Ordinary version
HZOJ-45: Longest Common Subsequence#

Sample Input
sehuaizexi
yhaizeyiux
Sample Output
6
- Thought
- State definition
- $dp(i,\ j)$: Represents the length of the longest common subsequence corresponding to the first i characters of the first string and the first j characters of the second string
- State transfer
- $dp(i) = \left{\begin{aligned}&max{dp(i-1,\ j),\ dp(i,\ j-1)} &s1(i)\neq s2(j)\&dp(i-1,\ j-1)+1&s1(i)=s2(j)\end{aligned}\right.$
- ⭐ The number of states involved in decision-making will change based on conditions
- Depends on whether the i-th position of string 1 and the j-th position of string 2 are equal
- The number of states to be decided is either 2 or 1, while the previous question had i states
- [PS]
- Situation 2 does not require decision-making, its value is certainly not less than situation 1, because in situation 1, $dp(i-1,\ j)$ or $f(i,\ j-1)$ is at most 1 greater than $f(i-1,\ j-1)$ in situation 2
- However, including situation 2 in the decision-making of situation 1 is certainly correct, i.e., under situation 2, $dp(i)=max{dp(i-1,\ j),\ dp(i,\ j-1),\ dp(i-1,\ j-1)+1}$
- Time complexity of state transfer: $O(n \times m)$
- State definition
- Code

- Simplified version: Can reduce one line of code, the value of situation 2 is certainly not less than situation 1
- Note: dp starts from dp[1][1], but string indexing starts from 0
Tips#
- Make a problem into a category of problems
- Quickly copy the entire line in vim — shift + v — visual line mode
- Some phenomena we may not understand, but do not easily deny them, because the smartest person is not us, existence is reasonable