—— 遞歸熱身 ——#
HZOJ-240:圖形打印 4#
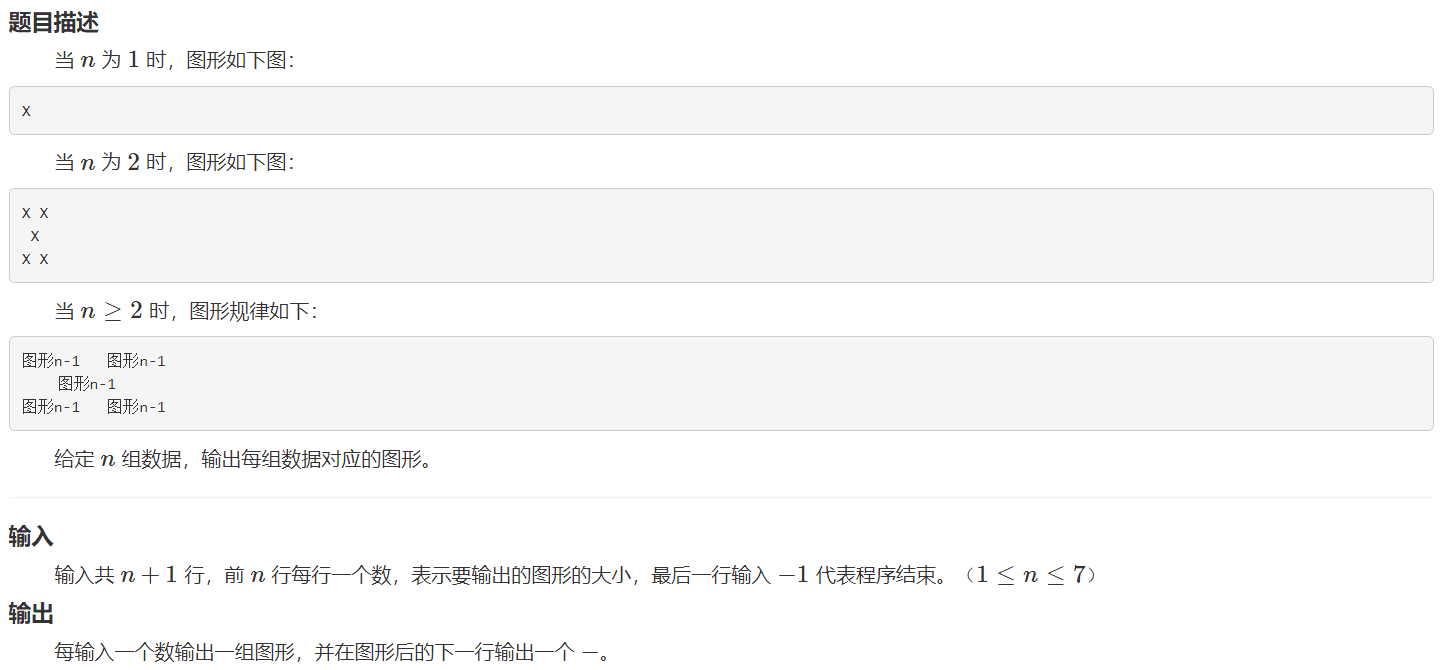
範例輸入
1
2
3
4
-1
範例輸出
X
-
X X
X
X X
-
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
-
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
-
- 思路
- 遞歸
- func (x, x, n):從點 (x, x) 開始,畫大小為 n 的圖形
- 邊界:當 n = 1 時,在點 (1, 1),畫 'x'
- 分解:func (x, x, n) 由 5 個有排列規律的 func (x', x', n - 1) 組成
- ⭐根據邊長預測 5 個部分的起始點的位置
- 邊長 L 是首項為 1,公比為 3 的等比數列
- 以左上角點為基準:其餘 3 個頂點的偏移量是 L / 3 * 2、中心點的偏移量是 L / 3
- ⭐根據邊長預測 5 個部分的起始點的位置
- 需要輸出多次,而 n 最大為 7
- 所以,直接存好 func (1, 1, 7) 的結果,根據輸入 n 輸出即可
- 代碼
-

- 先存好圖形數組,5 個部分的起始點位置
-
—— 排列組合 ——#
- 排列組合三兄弟:指數型、組合、全排列
- 延伸
- 【組合問題】對於 1 個數組 num [100],任選 5 個數,輸出和
- 【全排列問題】對於 1 個數組 num [100],輸出全排列
- 【組合 + 全排列】n 個數任選 m 個數,再對 m 個數全排列,即 236 + 237 組合練習
- 先組合,再對得到的組合數進行全排列
- 【3 兄弟自由組合】
- 延伸
- 時間複雜度都很高
- 全排列:O (n!)
HZOJ-235:遞歸實現指數型枚舉#

範例輸入
3
範例輸出
1
1 2
1 2 3
1 3
2
2 3
3
- 思路
- 按字典序排序
- 遞歸的每一層選一個數字
- 第 1 層:在 1 ~ n 中選
- 若某一層選出 i,則下一層:在 i + 1 ~ n 中選。注意:直接 + 1!
- 舉例:n = 4
第一層:1 2 3 4 中選→1
第二層:2 3 4 中選→2
第三層:3 4 中選→3
第四層:4 中選→4
- 代碼
- 第一版:func 函數用2 個參數,便於理解→從幾開始選 + 這是第幾層
-

- 用 num [15] 存前面已經存好的數,最多 10 個數
- 第二版:func 函數用1 個參數,更有回溯感→從幾開始選【把這是第幾層放到全局裡】
-

- 注意:與版本一不同,這裡的深度 cnt 是從 0 開始,版本一的 deep 是從 1 開始
- 深度從 1 還是 0 取決於自己,但自己在存值和輸出時要統一
HZOJ-236:遞歸實現組合型枚舉#

範例輸入
5 3
範例輸出
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
- 思路
- 類似上一題 [指數型枚舉],直接修改的話:增加輸出條件,存了 m 個數才輸出
- 同樣可用 2 個或 3 個參數:多一個輸出條件,存的深度達到 m 才輸出
- 2 個更有回溯感;3 個更易理解
- 代碼
- func 函數用 2 個參數版
-

- 可自己手寫體會
- 【經測試】實際上變量 cnt 或 left 中的一個可以不需要
- 不要 left:第 12 行,cnt 可由 m 代替;第 26 行,cnt 可由 m - left 代替;清除其他 cnt
- 但用 cnt 理解更清晰
HZOJ-237:遞歸實現排列型枚舉#

範例輸入
3
範例輸出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
- 思路
- 全排列
- 每一層都是 1~n:這一層與上一層沒關係
- 引入 mark 數組:標記已經選了哪些數了
- C++ 裡自帶全排列函數 next_permutation、prev_permutation
- 參考STL 中的全排列函數
- 但其實不是很好用,自己實現更靈活
- 全排列
- 代碼
-

- 添加標記數組,打標記操作和 cnt 加減操作的配合
-
—— 深搜 ——#
- 接上:遞歸👉排列組合👉搜索(深搜)
- 排列組合其實是深搜的一種
- 聯想樹的遍歷
- 往下搜:cnt++;往上回:cnt--
- ⭐主要解決【連通性】問題
- 兩個點是否相連,相連的點有哪些、有多少
- 解決最短路徑問題很費勁,需要遍歷所有路徑,可以找但沒必要
深搜走地圖 —— 基本模板#
- 方向數組:根據目前所在點可以得到下一點的位置,判斷是否可走、到達終點
- 存地圖:補 0,可以減少邊界判斷,如果用 vector 需要手動判斷邊界
- 遞歸、去重 [或標記數組]、補 0 [或判斷邊界]
代碼
-

-
每次拿到新的點,就以新的點為起點再搜 [遞歸]
-
走到終點會提前停止搜索,走不到的情況會把所有路徑都枚舉一遍
HZOJ-535:瓷磚#

範例輸入
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
範例輸出
59
- 思路
- 深搜、走到底;廣搜也能做
- 注意:輸入 h、w 的順序
- 範例為 9 行 11 列,輸入為 11 9
- 能走多少個 '.',用一個答案 ans 存,起始為 1
- 代碼
-

- 不需要返回值,統計全局變量 ans 即可
-
HZOJ-397:殭屍來襲#

範例輸入
5 6
0 1 2 3 4 0
1 0 0 0 0 0
2 9 3 0 2 4
0 0 2 0 2 8
1 0 0 0 0 0
範例輸出
4
- 思路
- 遍歷,找到一個非 0,波數 + 1,並以其為起點,【深搜】清除和它一波的殭屍
- 每經過一個非 0,就置為 0,避免之後的重複搜索
- 再下一波
- 非 0 值的數值大小在這裡沒有用,只管 0 / 非 0
- 遍歷,找到一個非 0,波數 + 1,並以其為起點,【深搜】清除和它一波的殭屍
- 代碼
-

- 連通性問題,注意去重、輸入地圖為 int 型
-
HZOJ-536:最大黑色區域#

範例輸入
5 6
011001
110101
010010
000111
101110
範例輸出
7
- 思路
- 上題為有幾片黑色區域,這題為最大的黑色區域有多大
- 記錄臨時最大值即可
- 注意
- 輸入的矩陣是字符,可以一次讀入一行:cin >> &mmap [i][1];
- 去重
- 代碼
-
HZOJ-396:填塗顏色⭐#

範例輸入
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
範例輸出
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
- 思路
- 只有 0、1
- 被 1 包住的 0 沒法判斷,但【沒被 1 包住的 0】可以判斷!
- ❗ 沒被 1 包住的 0 肯定與邊界相連
- 把沒被包住的 0 改成其他值:3
- 【輸出只管】遇到 3 輸出 0,遇到 0 輸出 2
- 如何找沒被 1 包住的 0 呢?
- ❌方法一:遍歷整個外圈,遇到 0 就深搜
-

- 【麻煩】0 有可能被 1 分割,有多片區域,所以要遍歷整個外圈
-
- ⭐方法二:補 0,找和左上角點 [0, 0] 點聯通的 0
-

- 【妙】這些 0 和沒被 1 包住的 0 全是連通的,可以一次搜索處理掉!
- 注意:必須嚴格判斷邊界
-
- ❌方法一:遍歷整個外圈,遇到 0 就深搜
- 代碼
-

- 注意判斷邊界、輸出判斷
-
HZOJ-404:01 迷宮簡易版#

範例輸入
2 3
011
100
2 3
範例輸出
2
- 思路
- 深搜,相當於求最大連通域
- 移動方式為:0→1,1→0。即不相同才能移動
- ⭐引入標記數組
- 【去重】該場景使用標記數組更方便,減少判斷次數
- 【不能補 0】0 在本題有特殊用途,需額外判斷邊界
- 代碼
-

- 標記數組的引入!
- 需要判斷邊界,因為搜索條件為不相同時繼續
- 雖然這裡像是補了 0,其實沒用到
-
HZOJ-405:01 迷宮⭐#

範例輸入
2 3 4
011
100
1 1
2 2
1 3
2 3
範例輸出
4
4
2
2
- 思路
- 深搜
- 與上題的區別:詢問次數很多!高達 30000 次
- 如果用上題方式,每來一個坐標求一次,必超時
- 👇空間【答案數組】換時間👇
- 需要額外的數組存每個點的答案:ans [3005][3005]
- ⭐此外,需要用隊列[方便,棧、數組都行] 存某個連通區域的點集合
- 只有搜索完這一個連通域才知道它們的答案 [相同的]
- 代碼
-

- ❗ 答案數組兼任標記數組去重
- 這裡,補 0 沒有作用,只是習慣從 1 開始讀了
- 隊列的 size () 其實也是當前的答案 temp
- 輸出,直接輸出答案數組對應坐標的值即可
-
—— 廣搜 ——#
-
同樣可解決【連通性】問題。如HZOJ-396:填塗顏色,思路見上
-

-
除了可以解決【連通性】問題外,還可以解決⭐【最短路徑】問題
- 從起點到終點最少需要多少步
- 最先搜到的點一定是最短的,因為是按層來的→層序遍歷
廣搜走地圖 —— 基本模板#
- 方向數組、存地圖
- 隊列 [必須]:存遍歷的點,而不需要遞歸;其元素為自定義結構,存坐標、當前步數
- 去重 [或標記數組]、補 0 [或判斷邊界]
代碼
-

-
關鍵:入隊出隊、自定義結構體
HZOJ-399:小明吃飯#

範例輸入
5 6
2.....
###.#.
....#.
..###.
....3.
範例輸出
10
- 思路
- 即廣搜走地圖 —— 基本模板
- 代碼
-

- 去重:改成非可走的字符 '.' 即可,如 0
-
HZOJ-304:騎士風度的牛#

範例輸入
10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
範例輸出
5
- 思路
- 像馬的走法
- 方向數組變成 8 個
- [1, 2] 和 [2, 1] 組合各四種
- 沒有憋腿的情況
- 注意越界問題:從 1, 1 點存還要判斷邊界,直接從 2, 2 點存
- 坑:先輸入列數
- 代碼
-

- 基本模板題,關鍵在方向數組變了
-
HZOJ-398:馬的遍歷#

範例輸入
3 3 1 1
範例輸出
0 3 2
3 -1 1
2 1 4
- 思路
- 從起點往外搜,仍為 8 個方向
- 【疑問】
- 是否是地圖?什麼障礙都沒有,就是一個數組
- 如何去重呢?同樣利用數組,判斷位置上的值
- 判斷邊界呢?基於數組,判斷方便
- 若不判斷,需把所有點右移下移一位考慮,且要把外面 2 圈做成障礙,麻煩!
- 一個大數組 num [405][405]:既存答案,又去重
- 【題意】不可達輸出 - 1,起點輸出 0
- 兩種初始化方式
- [孬] 初始化為 0:需要兩個特判,一個到不了的點 [0 → -1],起點 [0]
- 🆗初始化為 - 1:完美
- 代碼
-

- 題意裡的坐標是 [1, 1] 算起的,但還要判斷邊界,因為馬走法要預留 2 圈,且沒有將邊界設置障礙
- 用數組 num 代替地圖,還存答案、去重
- memset -1 是精髓
-
HZOJ-400:奇怪的象棋遊戲#

範例輸入
12 16
18 10
範例輸出
8
9
- 思路
- 棋盤大小固定為 500 * 500
- 12 個方向,2 次搜索,一個套路
- 代碼
- 注意第 2 次搜索的可能優化,碰見走過的點,直接用當前步數加上 [上一次搜索答案 - 存的步數]
- 直接看下一題,方法更有意思
HZOJ-401:奇怪的象棋遊戲升級版#

範例輸入
2
12 16
18 10
範例輸出
8
9
- 思路
- 搜索高達 2000 次,上題的思路肯定超時
- ⭐終點固定,從 [1, 1] 往外走,記錄一個答案數組
- 這裡從起點到終點和從終點到起點的答案一樣,注意根據題意來
- 思路反過來後,類似 OJ-398 題了
- 代碼
-

- 同樣 memset -1,考慮起點步數為 0
- 本題棋盤足夠大,不需要考慮走不到的情況,走不到一般是棋盤奇小
-
HZOJ-303:矩陣距離一#


範例輸入
3 4
0001
0011
0110
範例輸出
3 2 1 0
2 1 0 0
1 0 0 1
- 思路
- 輸入:char!待會判斷邊界可用
- 這個距離其實就是一個一個走的步數
- 同上題思路,終點變起點,但有多個起點,且本題有輸入地圖
-

- 從每個起點開始,依次 4 個方向走 1 步,走完就下一位
-
- 代碼
-

- 同樣,memset 初始化 num 為 - 1
- 通過答案數組去重,地圖保持不變
- 答案數組可以和地圖統一為一個嗎?不行,輸出需要用到答案數組,方便輸出 - 1,也方便理解
-
HZOJ-305:乳草的入侵#

範例輸入
4 3 1 1
....
..*.
.**.
範例輸出
4
- 思路
- 輸入:行列數調換、起點坐標 (1, 1) 是左下角的格
- 起點坐標同樣也是反的
- 把 (1, 1) 點當作 (Y, 1) 點
- 原則:以我們常用的坐標系為準,調整到我們的坐標系中
- 8 個方向
- ⭐新的套路:沒有終點,遍歷完就是結果
- 終止狀態:隊列為空
- 如何記錄最遠步數?用一個變量!
- 輸入:行列數調換、起點坐標 (1, 1) 是左下角的格
- 代碼
-

- 注意輸入、去重、最遠的步數記錄
-
HZOJ-529:龍與蟲#

範例輸入
3 4
OXXO
XXOO
XOOO
3 2 2 4
3 3 1 1
0 0 0 0
範例輸出
1
Impossible!
- 思路
- [孬] 直接從起點廣搜;每走一步就判斷:通過方向數組循環 + 1,再一一做判斷,判斷非常多
- ⭐反轉思維,但又不完全反轉
- 先從敵人出發,通過方向數組標記所有能被直接幹掉的點,作為【終點集合】
- 再從起點廣搜,只有當蟲子【移動到】終點集合裡才能幹掉敵人,輸出此時的步數
- 多組數據,使用標記數組
- 原地圖不能變,還需要用
- 開額外的數組做標記:用 1 標記終點、用 2 標記走過的點
- 對每組數據,重新創建該數組或清空皆可
- 標記敵人是關鍵
- 代碼
-

-

- 題意:坐標從 [1, 1] 開始
- 對於【多組輸入】數據,封裝成函數,否則需要用 flag 標志是否結束,因為會有兩層循環
- 標記數組是局部變量,對於每次輸入數據都是全新的
- 廣搜或方向數組遍歷的時候別忘記【自己】的情況,因為其判斷不到
- 不標記起點也沒錯,但是多走一次起點
-
HZOJ-527:飛躍原野#

範例輸入
4 4 2
PLLP
PPLP
PPPP
PLLP
範例輸出
5
- 思路
- 起點:[1, 1];終點:[m, n]
- 飛行距離有限,為 D,等同於總能量
- 【1】去重需要增加一個維度:剩餘能量
- 因為:數據範圍小 100;且不同剩餘能量對於不同的可能走法,需區分
- 創建三維數組:點的坐標 x y、剩餘能量
- 元素值 [標記]:就用 0、1 即可
- 自定義結構也多一維,記錄此時的剩餘能量
- 【2】走 or 飛
- 飛的範圍:2 ~ 剩餘能量,只有 ≥ 2 步的飛才有意義,不然走還省能量
- 代碼

- 【關注】增加剩餘能量維度去重、飛的方式
- 注意:飛裡面是 break
- [PS] 在能量足夠的時候,這種暴力枚舉的方式其實會有一些無效的【回飛】的情況,但是也只會在最優的步數裡走出無效的情況。這實際上是由三維去重數組導致的
雖然對某個剩餘能量的坐標去重了,但對於 PPPPP (12345) 這樣的情況,如果能量足夠,會有 1-3-5-3-5-3 這樣的走法
附加知識點#
- C++ 裡自帶全排列函數 next_permutation、prev_permutation
- 參考STL 中的全排列函數
- 但其實不是很好用,自己實現更靈活
思考點#
⭐搜索套路:5 步走#
- 存、起、終、轉、重【詳見下一章:7 搜索綜合問題】
Tips#
- 尋路算法:可以參考A * 搜索算法——Wiki,等


