—— 再帰のウォームアップ ——#
HZOJ-240:図形印刷 4#
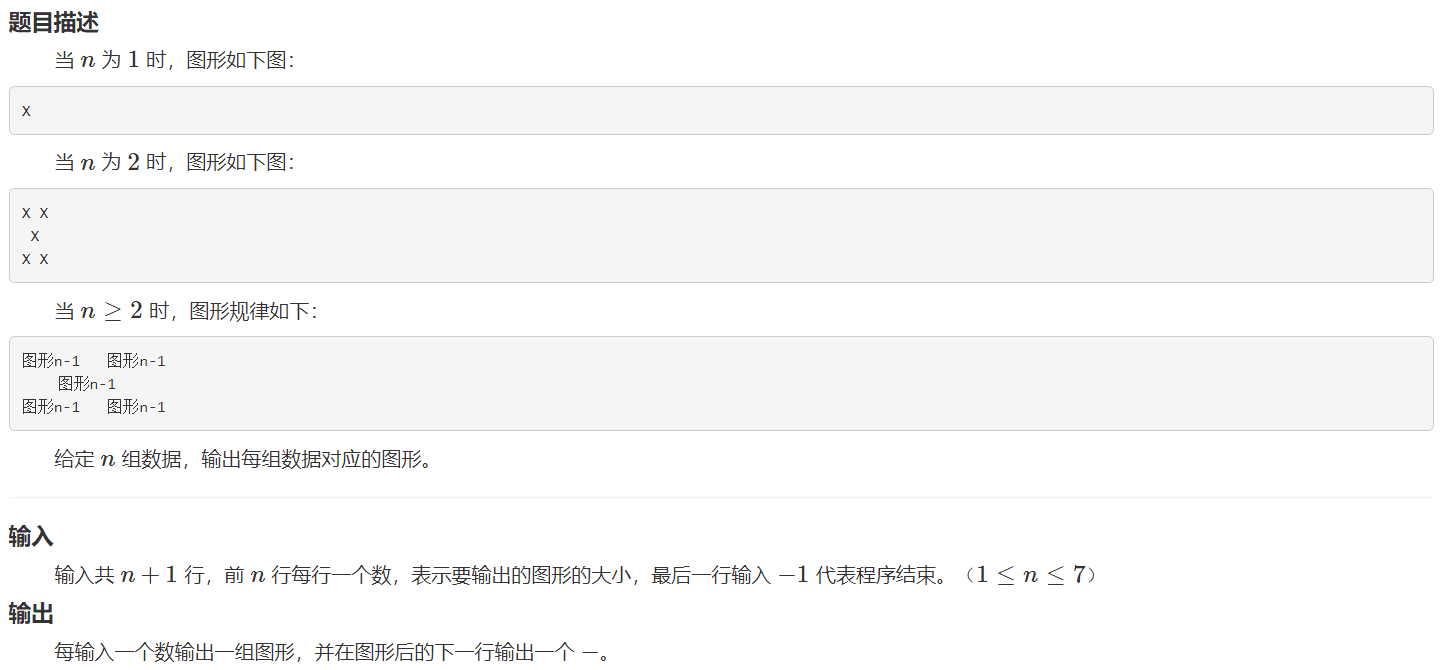
サンプル入力
1
2
3
4
-1
サンプル出力
X
-
X X
X
X X
-
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
-
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
-
- 思路
- 再帰
- func (x, x, n):点 (x, x) から始めて、サイズ n の図形を描く
- 境界:n = 1 のとき、点 (1, 1) に 'x' を描く
- 分解:func (x, x, n) は 5 つの排列規則を持つ func (x', x', n - 1) から構成される
- ⭐辺の長さに基づいて 5 つの部分の開始点の位置を予測する
- 辺の長さ L は初項が 1 で、公比が 3 の等比数列
- 左上の点を基準に:他の 3 つの頂点のオフセットは L / 3 * 2、中心点のオフセットは L / 3
- ⭐辺の長さに基づいて 5 つの部分の開始点の位置を予測する
- 複数回出力する必要があり、n の最大値は 7
- したがって、func (1, 1, 7) の結果を直接保存し、入力 n に基づいて出力する
- コード
-

- 5 つの部分の開始点位置を保存した図形配列を先に保存する
-
—— 排列组合 ——#
- 排列组合三兄弟:指数型、组合、全排列
- 延伸
- 【组合問題】1 つの配列 num [100] から任意の 5 つの数を選び、合計を出力する
- 【全排列問題】1 つの配列 num [100] から全排列を出力する
- 【组合 + 全排列】n 個の数から m 個の数を選び、m 個の数を全排列する、つまり 236 + 237 の組み合わせ練習
- 先に組み合わせ、その後得られた組み合わせ数を全排列する
- 【3 兄弟自由組み合わせ】
- 延伸
- 時間計算量は非常に高い
- 全排列:O (n!)
HZOJ-235:再帰による指数型列挙の実装#

サンプル入力
3
サンプル出力
1
1 2
1 2 3
1 3
2
2 3
3
- 思路
- 辞書順にソート
- 再帰の各レベルで 1 つの数字を選ぶ
- 第 1 レベル:1 ~ n から選ぶ
- あるレベルで i を選んだ場合、次のレベル:i + 1 ~ n から選ぶ。注意:直接 + 1!
- 例:n = 4
第一レベル:1 2 3 4 から選ぶ→1
第二レベル:2 3 4 から選ぶ→2
第三レベル:3 4 から選ぶ→3
第四レベル:4 から選ぶ→4
- コード
- 第一版:func 関数は2 つのパラメータを使用し、理解しやすくする→どこから選ぶか + これは何レベルか
-

- num [15] を使用して、前に保存した数を最大 10 個保存する
- 第二版:func 関数は1 つのパラメータを使用し、よりバックトラック感を出す→どこから選ぶか【これは何レベルかをグローバルにする】
-

- 注意:バージョン 1 と異なり、ここでの深さ cnt は 0 から始まる、バージョン 1 の deep は 1 から始まる
- 深さは 1 から 0 を選ぶかは自分次第だが、値を保存し出力する際は統一する必要がある
HZOJ-236:再帰による組み合わせ型列挙の実装#

サンプル入力
5 3
サンプル出力
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
- 思路
- 前の問題 [指数型列挙] に似て、直接修正する場合:出力条件を追加し、m 個の数を保存したら出力する
- 同様に 2 つまたは 3 つのパラメータを使用できる:出力条件を追加し、保存の深さが m に達したら出力する
- 2 つの方がバックトラック感が強い;3 つの方が理解しやすい
- コード
- func 関数は 2 つのパラメータ版
-

- 自分で手書きして体験することができる
- 【テスト済み】実際には変数 cnt または left の 1 つは不要
- left を使わない:12 行目では cnt は m で代用できる;26 行目では cnt は m - left で代用できる;他の cnt をクリアする
- しかし cnt を使うことで理解がより明確になる
HZOJ-237:再帰による排列型列挙の実装#

サンプル入力
3
サンプル出力
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
- 思路
- 全排列
- 各レベルは 1~n:このレベルは前のレベルとは関係ない
- mark 配列を導入:どの数が選ばれたかをマークする
- C++ には自動的に全排列関数 next_permutation、prev_permutation がある
- 参考STL の全排列関数
- しかし実際にはあまり使えず、自分で実装する方が柔軟である
- 全排列
- コード
-

- マーク配列を追加し、マーク操作と cnt の加減操作の組み合わせ
-
—— 深さ優先探索 ——#
- 引き続き:再帰👉排列组合👉探索(深さ優先探索)
- 排列组合は実際には深さ優先探索の一種である
- 木の遍歴を連想する
- 下に探索:cnt++;上に戻る:cnt--
- ⭐主に【連結性】問題を解決する
- 2 つの点が接続されているか、接続されている点はどれか、いくつあるか
- 最短経路問題を解決するのは非常に手間がかかり、すべての経路を遍歴する必要があるが、探すことはできるが必要ではない
深さ優先探索の地図を歩く —— 基本テンプレート#
- 方向配列:現在の点に基づいて次の点の位置を得て、移動可能か、終点に到達できるかを判断する
- 地図を保存:0 を補充し、境界判断を減らすことができる。vector を使用する場合は手動で境界を判断する必要がある
- 再帰、重複排除 [またはマーク配列]、0 を補充 [または境界を判断]
コード
-

-
新しい点を取得するたびに、その新しい点を起点に再度探索する [再帰]
-
終点に到達すると検索が早期に停止し、到達できない場合はすべての経路を列挙する
HZOJ-535:タイル#

サンプル入力
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
サンプル出力
59
- 思路
- 深さ優先探索、最後まで行く;広さ優先探索でもできる
- 注意:入力 h、w の順序
- サンプルは 9 行 11 列、入力は 11 9
- いくつの '.' を移動できるか、1 で初期化した ans を使用する
- コード
-

- 戻り値は必要なく、グローバル変数 ans を統計するだけでよい
-
HZOJ-397:ゾンビ襲来#

サンプル入力
5 6
0 1 2 3 4 0
1 0 0 0 0 0
2 9 3 0 2 4
0 0 2 0 2 8
1 0 0 0 0 0
サンプル出力
4
- 思路
- 遍歴し、非 0 を見つけたら波数を + 1 し、それを起点に【深さ優先探索】でその波のゾンビを消去する
- 非 0 を通過するたびに 0 に設定し、後の重複検索を避ける
- 次の波へ
- 非 0 値の数値の大きさはここでは関係なく、0 / 非 0 だけを考慮する
- 遍歴し、非 0 を見つけたら波数を + 1 し、それを起点に【深さ優先探索】でその波のゾンビを消去する
- コード
-

- 連結性問題、重複排除に注意、入力地図は int 型
-
HZOJ-536:最大黒色領域#

サンプル入力
5 6
011001
110101
010010
000111
101110
サンプル出力
7
- 思路
- 前の問題は黒色領域の数、今回は最大の黒色領域の大きさ
- 一時的な最大値を記録するだけでよい
- 注意
- 入力の行列は文字で、一度に 1 行を読み込むことができる:cin >> &mmap [i][1];
- 重複排除
- コード
-
HZOJ-396:色を塗る⭐#

サンプル入力
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
サンプル出力
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
- 思路
- 0 と 1 のみ
- 1 に囲まれた 0 は判断できないが、【1 に囲まれていない 0】は判断できる!
- ❗ 1 に囲まれていない 0 は必ず境界に接続されている
- 1 に囲まれていない 0 を他の値に変更する:3
- 【出力は】3 に出会ったら 0 を出力し、0 に出会ったら 2 を出力する
- どうやって 1 に囲まれていない 0 を見つけるか?
- ❌方法一:外周全体を遍歴し、0 に出会ったら深さ優先探索を行う
-

- 【面倒】0 は 1 によって分割される可能性があり、多くの領域を遍歴する必要がある
-
- ⭐方法二:0 を補充し、左上の点 [0, 0] と連結している 0 を探す
-

- 【妙】これらの 0 はすべて連結しており、一度の探索で処理できる!
- 注意:必ず境界を厳密に判断する
-
- ❌方法一:外周全体を遍歴し、0 に出会ったら深さ優先探索を行う
- コード
-

- 境界を判断し、出力を判断することに注意
-
HZOJ-404:01 迷路簡易版#

サンプル入力
2 3
011
100
2 3
サンプル出力
2
- 思路
- 深さ優先探索、最大連結域を求める
- 移動方法は:0→1、1→0。つまり異なる場合にのみ移動できる
- ⭐マーク配列を導入
- 【重複排除】このシーンではマーク配列を使用する方が便利で、判断回数を減らす
- 【0 を補充できない】0 はこの問題で特別な用途があり、境界を追加で判断する必要がある
- コード
-

- マーク配列の導入!
- 境界を判断する必要がある、検索条件は異なる場合に続行する
- ここでは 0 を補充したように見えるが、実際には使用されていない
-
HZOJ-405:01 迷路⭐#

サンプル入力
2 3 4
011
100
1 1
2 2
1 3
2 3
サンプル出力
4
4
2
2
- 思路
- 深さ優先探索
- 前の問題との違い:問い合わせの回数が非常に多い!最大 30000 回
- 前の問題の方法を使用すると、各座標が来るたびに求めると必ずタイムアウトする
- 👇空間【答え配列】を時間に変える👇
- 各点の答えを保存するために追加の配列が必要:ans [3005][3005]
- ⭐さらに、特定の連結領域の点の集合を保存するためにキューが必要 [便利で、スタックや配列でも可]
- この連結域を探索し終えるまで、その答えを知ることはできない [同じである]
- コード
-

- ❗ 答え配列はマーク配列の重複排除も兼ねている
- ここでは 0 を補充することは効果がなく、単に 1 から読み始める習慣である
- キューの size () は実際には現在の答え temp でもある
- 出力は、答え配列に対応する座標の値を直接出力すればよい
-
—— 広さ優先探索 ——#
-
同様に【連結性】問題を解決できる。例えばHZOJ-396:色を塗る、思路は上記の通り
-

-
【連結性】問題を解決できるだけでなく、⭐【最短経路】問題も解決できる
- 起点から終点までの最小ステップ数はどれか
- 最初に探索した点は必ず最短である。なぜなら層ごとに来るから→層順遍歴
幅優先探索の地図を歩く —— 基本テンプレート#
- 方向配列、地図を保存
- キュー [必須]:遍歴する点を保存し、再帰する必要はない;その要素はカスタム構造体で、座標と現在のステップ数を保存する
- 重複排除 [またはマーク配列]、0 を補充 [または境界を判断]
コード
-

-
重要:キューへの入出力、自分で定義した構造体
HZOJ-399:小明の食事#

サンプル入力
5 6
2.....
###.#.
....#.
..###.
....3.
サンプル出力
10
- 思路
- つまり、幅優先探索の基本テンプレート
- コード
-

- 重複排除:移動可能でない文字 '.' に変更するだけでよい、例えば 0
-
HZOJ-304:騎士の風格の牛#

サンプル入力
10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
サンプル出力
5
- 思路
- 馬の動きのように
- 方向配列を 8 つに変更
- [1, 2] と [2, 1] の組み合わせがそれぞれ 4 つ
- 足が詰まる状況はない
- 境界問題に注意:1, 1 点から保存し、境界を判断する必要がある。直接 2, 2 点から保存する
- 注意:列数を先に入力する
- コード
-

- 基本テンプレートの問題で、重要なのは方向配列が変わったこと
-
HZOJ-398:馬の遍歴#

サンプル入力
3 3 1 1
サンプル出力
0 3 2
3 -1 1
2 1 4
- 思路
- 起点から外に探索し、依然として 8 つの方向
- 【疑問】
- 地図なのか?障害物が何もない、ただの配列
- どうやって重複排除するのか?同様に配列を利用し、位置の値を判断する
- 境界を判断するには?配列に基づいて、判断が容易
- 判断しない場合、すべての点を右に下に移動させる必要があり、外側の 2 つの円を障害物にする必要があるので面倒!
- 大きな配列 num [405][405]:答えを保存し、重複排除も行う
- 【問題意】到達できない場合は - 1 を出力し、起点は 0 を出力する
- 2 つの初期化方法
- [悪い] 初期化を 0 にする:特別なケースが 2 つ必要、到達できない点 [0 → -1]、起点 [0]
- 🆗初期化を - 1 にする:完璧
- コード
-

- 問題意の座標は [1, 1] から始まるが、境界を判断する必要がある。馬の動きのために 2 つの円を残す必要がある
- 配列 num を地図の代わりに使用し、答えを保存し、重複排除も行う
- memset -1 は精髄
-
HZOJ-400:奇妙なチェスゲーム#

サンプル入力
12 16
18 10
サンプル出力
8
9
- 思路
- チェス盤のサイズは 500 * 500 に固定
- 12 の方向、2 回の探索、1 つのパターン
- コード
- 2 回目の探索の可能な最適化に注意。訪れた点に遭遇した場合、現在のステップ数に加え [前回の探索の答え - 保存したステップ数] を直接使用する
- 次の問題を直接見て、方法がより面白い
HZOJ-401:奇妙なチェスゲームのアップグレード版#

サンプル入力
2
12 16
18 10
サンプル出力
8
9
- 思路
- 探索は 2000 回に達する。前の問題の思路は必ずタイムアウトする
- ⭐終点は固定されており、[1, 1] から外に向かって移動し、答え配列を記録する
- ここでは起点から終点までの答えと終点から起点までの答えは同じである。問題意に基づいて注意する
- 思路を逆にすると、OJ-398 の問題に似ている
- コード
-

- 同様に memset -1、起点のステップ数を 0 と考慮する
- この問題のチェス盤は十分大きいため、到達できない状況を考慮する必要はない。到達できないのは通常チェス盤が非常に小さい場合
-
HZOJ-303:行列距離 1#


サンプル入力
3 4
0001
0011
0110
サンプル出力
3 2 1 0
2 1 0 0
1 0 0 1
- 思路
- 入力:char!後で境界判断に使用できる
- この距離は実際には 1 つずつ移動するステップ数である
- 前の問題の思路と同様に、終点が起点に変わるが、複数の起点があり、さらにこの問題には入力地図がある
-

- 各起点から始めて、順に 4 つの方向に 1 ステップ移動し、移動が完了したら次の位置に移動する
-
- コード
-

- 同様に、memset で num を - 1 に初期化
- 答え配列を使用して重複排除し、地図はそのままにしておく
- 答え配列を地図と統一することはできない。出力には答え配列を使用する必要があり、-1 を出力するのも理解しやすい
-
HZOJ-305:乳草の侵入#

サンプル入力
4 3 1 1
....
..*.
.**.
サンプル出力
4
- 思路
- 入力:行列数を入れ替え、起点座標 (1, 1) は左下の格子
- 起点座標も反転する
- (1, 1) 点を (Y, 1) 点と見なす
- 原則:私たちが一般的に使用する座標系に基づいて、私たちの座標系に調整する
- 8 つの方向
- ⭐新しいルール:終点がない、すべてを遍歴することが結果である
- 終了状態:キューが空
- 最も遠いステップ数を記録するには、1 つの変数を使用する!
- 入力:行列数を入れ替え、起点座標 (1, 1) は左下の格子
- コード
-

- 入力、重複排除、最も遠いステップ数の記録に注意
-
HZOJ-529:ドラゴンと虫#

サンプル入力
3 4
OXXO
XXOO
XOOO
3 2 2 4
3 3 1 1
0 0 0 0
サンプル出力
1
Impossible!
- 思路
- [悪い] 直接起点から広さ優先探索;移動するたびに判断:方向配列をループ + 1 し、1 つずつ判断する必要がある
- ⭐逆転思考だが完全に逆転するわけではない
- 先に敵から出発し、方向配列を通じて直接排除できる点をすべてマークし、【終点集合】として扱う
- 次に起点から広さ優先探索を行い、虫が【移動して】終点集合に到達できる場合にのみ敵を排除し、その時のステップ数を出力する
- 複数のデータセットを使用し、マーク配列を使用する
- 原地図は変更できず、使用する必要がある
- 追加の配列を使用してマークする:1 で終点をマークし、2 で通過した点をマークする
- 各データセットに対して、この配列を再作成するか、クリアすることができる
- 敵をマークすることが重要
- コード
-

-

- 問題意:座標は [1, 1] から始まる
- 【複数の入力】データに対して、関数に封装する。そうでなければ、終了フラグを使用する必要がある。なぜなら 2 重ループがあるから
- マーク配列はローカル変数であり、各入力データに対して全く新しいものである
- 幅優先探索や方向配列の遍歴の際には、自分自身の状況を忘れないでください。なぜならその判断はできないから
- 起点をマークしなくても問題はないが、起点をもう一度通過することになる
-
HZOJ-527:原野を飛び越える#

サンプル入力
4 4 2
PLLP
PPLP
PPPP
PLLP
サンプル出力
5
- 思路
- 起点:[1, 1];終点:[m, n]
- 飛行距離は有限で、D に等しい。つまり総エネルギー
- 【1】重複排除には次元を追加する必要がある:残りのエネルギー
- なぜなら:データ範囲は小さく 100;かつ異なる残りエネルギーは異なる移動方法を区別する必要がある
- 3 次元配列を作成する:点の座標 x y、残りエネルギー
- 要素値 [マーク]:0、1 を使用する
- カスタム構造体も 1 次元追加し、この時の残りエネルギーを記録する
- 【2】移動または飛ぶ
- 飛ぶ範囲:2 ~ 残りエネルギー、≥ 2 ステップの飛行のみが意味を持つ。そうでなければ歩く方がエネルギーを節約する
- コード

- 【注目】残りエネルギー次元を追加して重複排除し、飛ぶ方法
- 注意:飛ぶ際には break が必要
- [PS] エネルギーが十分な場合、このような暴力的な列挙方法は実際には無効な【逆飛び】の状況がいくつか発生するが、最適なステップ数の中で無効な状況を歩くことになる。これは実際には 3 次元の重複排除配列によるものである
ある残りエネルギーの座標を重複排除したが、PPPPP (12345) のような状況がある場合、エネルギーが十分であれば、1-3-5-3-5-3 のような移動方法がある
附加知識点#
- C++ には自動的に全排列関数 next_permutation、prev_permutation がある
- 参考STL の全排列関数
- しかし実際にはあまり使えず、自分で実装する方が柔軟である
思考点#
⭐探索のルール:5 ステップで進む#
- 保存、起点、終点、転換、重複【詳細は次の章:7 探索の総合問題を参照】
ヒント#
- 探索アルゴリズム:参考A * 探索アルゴリズム——Wiki など


