多模匹配問題,與字符串匹配相關的數據結構
課程內容#
多模匹配問題
有多個模式串的匹配問題,常規思路如下:
- Step1:多個模式串,建立成一棵字典樹
- Step2:和文本串的每一位對齊匹配,模擬暴力匹配的過程
Trie#
又名字典樹、單詞查找樹,顧名思義
看圖理解#
-

- 思考樹的含義:結點代表集合,邊代表關係
- 根結點可以理解為整個字典,第一個字母為 'a' 的單詞放在第一個子樹中,第一個字母為 'c' 的單詞放在第二個子樹中,以此類推
- 紅色結點,代表從根結點到當前結點的路徑上,經過的字母獨立成詞
- 當代表某字母的邊存在時 [指向一個結點],表示存在以之前字母為前綴的單詞集合
- [PS] 又名前綴樹:每個字符串是按照前綴的順序插入到該樹形結構中的
常用場景#
- ① 單詞查找
- 根據代表某字母的邊是否指向一個結點,判斷某字母是否存在,從而查找一個單詞
- ② 字符串排序
- 通過深度優先遍歷一棵字典樹,遇到成詞標記輸出字符串,即可完成字符串的有序輸出
- 時間複雜度:$O (n)$,沒有字符串大小比較
- ③ 多模匹配
- 一個字典樹可以代表多個模式串,遍歷文本串每一位,依次匹配字典樹中的字符串,即可完成多模匹配
- 但該方式本質上是多模匹配下的暴力匹配方式
暴力匹配下的思考#
-

- 首先思考暴力匹配過程
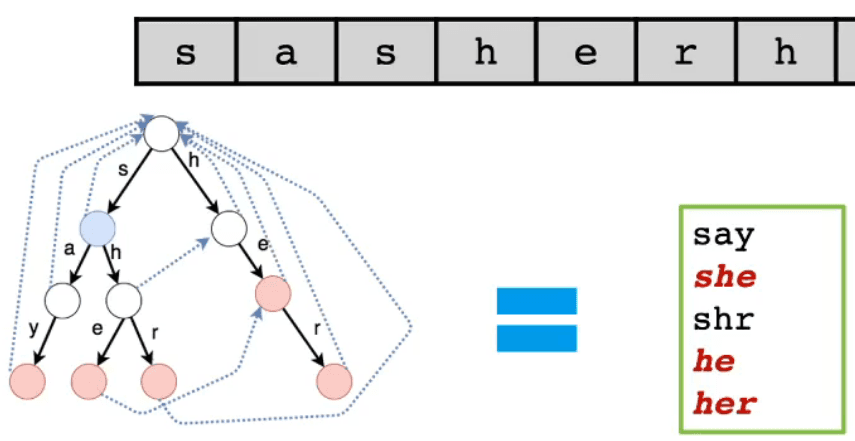
- 當使用字典樹成功匹配了文本串的 "she" 後,字典樹再向下走一位,嘗試匹配文本串的後一位 'r'
- 但此時字典樹下面已經沒有結點了,匹配失敗
- 文本串指針回溯到 'h',字典樹指針回到根結點繼續嘗試匹配,然後再成功匹配 "her"
- 上述過程有一個明顯的重複匹配過程
- 在成功匹配了 "she" 後,其實等價成功匹配了 "he"
- 所以在文本串指針後移一位時,實際上應該可以成功匹配 "her"
- 這其中就包含一種等價匹配關係[見下圖紅線]
-

- 當字典樹下方沒有匹配的結點時,還可以看看等價匹配關係那邊能不能匹配
- ❗ 是否可以通過等價匹配關係邊加速匹配過程呢?AC 自動機給出了答案 👇
-
AC 自動機#
狀態機思想,解決多模匹配問題的效率問題
AC = Trie + fail [等價關係]
建立等價匹配關係#
加速匹配過程
-

- ① 對於每一個子結點,其默認等價匹配關係是根結點
- ② 建立子結點的等價匹配關係時,會借助父結點的等價關係
- 如果找不到,還會往爺爺結點的等價關係找,直到到達根結點
- ❗ 不斷往上找等價關係的思想和 KMP 中 $next$ 數組的建立思想一模一樣,可跳轉:《高級數據結構》——4 字符串匹配算法(上)
- 例如:在找's'->'h' 的 'h' 的等價匹配關係時,會根據其父結點's' 的等價匹配關係 [即根結點] 找等價匹配關係,而根結點下方恰好有 'h',所以建立了等價匹配關係 $A$
- 注意
- 建立等價匹配關係時,要保證該結點上層的等價匹配關係已經建立,所以可以採用層序遍歷的方式,使用隊列
- 等價匹配關係通常叫做 $fail$ 指針
匹配過程#
在當前狀態下匹配字符,匹配失敗就到等價匹配關係上去匹配
- ① 狀態轉移
- 例如:"sas",在匹配第二個's' 時匹配失敗,所以會回到等價匹配關係 —— 根結點,再次嘗試匹配's';直到成功匹配,或等價匹配關係為空 [即根結點也找不到]
- [PS] 在程序實現中,根結點的等價匹配關係設為 NULL 更方便
- ② 取詞
- 匹配到成詞標記後,還需要往上判斷等價匹配關係的成詞標記
- 例如:當成功匹配文本串中的單詞 "she" 時,也意味著成功匹配等價關係上的單詞 "he"
- 思考:此時的 AC 自動機,本質上是一個NFA[非確定性有窮自動機]
- [假設:"she" 對應了字典樹中的結點 $P$,"he" 對應了字典樹中的結點 $Q$]
- 性質 1:當前狀態 $p$,在輸入字符 $c$ 後,無法通過一步操作確定下一狀態【滿足】
- 性質 2:當前狀態 $p$,並不代表唯一狀態 [也代表在狀態 $q$]【滿足】
- 時間複雜度:$O (k\times n)$,有一個很大的常數
- 因為匹配過程中,通過等價關係向上跳的次數不固定
- 是否可以優化呢?基於路徑壓縮思想,見下
優化#
讓狀態轉移過程一步到位
- 思考:狀態轉移時,根據等價關係向上跳的過程,是否可以一步到位呢?
-

- 當前狀態為 $p$,圖左為 $p$ 的等價關係 [$fail$]
- 在前面過程中,圖右中的紅色箭頭→,需要通過 $fail$ 指針做中間跳轉
- 【目標】實現紅色箭頭的一步到位
-
- 優化:廢物利用⭐
-

- $p$ 的 $next$ 數組中,$b$ 和 $c$ 本來對應空結點,純屬浪費,那為什麼不把它們用來指向等價關係的相應結點呢?同理,$p'$ 也是如此
- ❗ 注意可傳遞性:$p$ 指向 $c$ 的邊,可通過 $p'$ 指向 $c$ 的邊傳遞 [層序遍歷,$p'$ 指向 $c$ 的關係已獲得],所以在建立匹配關係的優化過程中,實際上不用根據 $fail$ 關係向上跳
-
- 此時的 AC 自動機,本質上接近DFA[確定有窮狀態自動機]
- 性質 1:當前狀態 $p$,在輸入字符 $c$ 後,可以通過一步操作跳轉到下一狀態【滿足】
- 性質 2:當前狀態 $p$,只代表唯一狀態【不滿足】
- 還是存在等價關係,只是跳轉可一步到位
- 時間複雜度:$O (n)$
Double-Array Trie#
雙數組字典樹,顧名思義,用兩個數組代表一棵字典樹
引入#
- 完全二叉樹
- 思維邏輯中的樹形結構,實際的存儲結構是一段連續的數組空間
- 相比普通二叉樹:節省了大量存儲邊的空間 [記錄左 / 右子孩子的地址]
- 優化思想:記錄式 👉 計算式,節省空間
- n 個結點的字典樹
- 開闢了 $BASE \times n$ 條邊的空間
- 但只使用其中的 $n - 1$ 條邊
- 故浪費了 $BASE \times n - (n - 1) = (BASE - 1) \times n + 1$ 條邊的空間
- 👉 參考完全二叉樹的優點,提出雙數組字典樹
- 同樣通過計算獲得子結點的地址,而不用存儲邊的信息
base 數組#
存儲基準值
- 【幫助父結點找到子結點】
- $base [i]$:第 $i$ 個結點存儲的 $base$ 值
- 它的第 $j$ 個子結點的下標等於 $base [i] + j$
- [PS]$base$ 值是自行設置的,可負,可重複
- 思考:如果只有 $base$ 數組,會有如下場景
-

- ❌ 兩個結點有編號相同的子結點,即 11 號結點可能對應多個父結點 [3、5]
- 所以需要確保設置 $base$ 值後,計算的子結點下標不與已使用的下標衝突
check 數組#
記錄父結點的索引
- 【親子鑑定,檢查結點的父結點究竟是誰】
- $check [i]$:第 $i$ 個結點的父結點下標
- 當通過 $base$ 值計算的子結點下標已有爸爸時,可更換 $base$ 值
- ❗ 思考:如何記錄成詞結點
- $base$ 值可任意設置
- 而 $check$ 值代表的是下標,一定非負,又可讓下標從 1 開始 [根結點]
- 👉 可用 $check$ 值的正負表示是否成詞
- [PS]$check [i]=0$ 可代表下標 i 還沒有被使用
公式化#
- $child_j = base[father] + j$
- $check [child_j] = \left {\begin {aligned}&father & 不成詞 \&-father & 成詞 \&0 & 無父親 \end {aligned}\right.$
- [PS]
- $child_j$:第 $j$ 子結點下標,$j$ 可對應一個字符信息
- $father$:父結點下標
- $root = 1$,$check[1] = 0$
小結#
- 通過兩個數組存儲字典樹的兩個重要信息
- ① 父子結點之間的樹形結構關係 [$base$+$check$]
- ② 結點是否獨立成詞 [$check$]
- 從而節省了大量邊的存儲空間
- 一個字典樹👉多個雙數組,一個雙數組👉一顆完整的字典樹
- 此時,字典樹也只是思維邏輯中的樹形結構,實際存儲的是兩段連續的數組空間
- ❗ 離線存儲結構
- 很方便傳輸、還原
- 但動態插入極其浪費時間
- 實際使用時,一次建立,多次使用 [查詢]
+ 二叉字典樹#
顧名思義,每個結點只有兩個分支
- 插入二進制串的字典樹,可插入任意信息 [計算機中任何信息都可以看成一個二進制串]
- 極其節省空間,但浪費時間
- 減少了寬度,增加了深度
- 本質:時間換空間
- ⭐ 二叉字典樹 + 哈夫曼編碼
- 在節省空間的同時,最大限度節省了查找時間 [減少深度]
代碼演示#
Trie#


- 上為字典樹的標準數據結構式的代碼實現,用於刷題的技巧性實現方式見下 [HZOJ-282]
- 結構定義
- 對於 26 個字母,結點中對應存儲 26 個結點,可理解為代表字母信息的 26 條邊
- 通過 $flag$,標記成詞結點
- 結構操作
- 插入單詞不會改變根結點地址,所以函數返回值為 void
- 存在指向某索引的結點,就代表存在對應的字母信息
- ⭐字符串排序
- 通過 $k$ 指示當前所在層數,$s$ 存儲字符串信息,通過每次在末尾置 0,隨時準備輸出字符串
- 利用遞歸的方式進行深度優先遍歷,關鍵在於理解 $k$
AC 自動機#
普通版#
$next$ 數組未充分利用




- 建立 Trie 樹 👉 建立等價匹配關係 [隊列、$fail$] 👉 匹配 [狀態轉移、取詞]
- 注意
- 根據等價關係向上跳的操作,不僅發生在建立和使用匹配過程中,還發生在取詞過程中
- 建立和使用等價匹配關係的 while 循環,耗時很大,可優化
- [思考:建立等價關係過程] 根結點的子結點的等價匹配關係必然指向根結點

- 第 64 行若使用 if,則需考慮第一次循環 $p$ 為 root 的情況
- $c$ 為 root 的子結點,$k$ 直接為 NULL,在第 60 行會直接跳出 while 循環,在第 62 行 k 賦值為 root,但第 64 行若用 if,root->next [i] 必然成立,因為就是 root 的子結點自身
- 在這裡,可以將根結點的子結點統一考慮,但在優化版中還是需要單獨拿出來做處理
優化版#
充分利用 $next$ 數組,建立和匹配過程都得到了優化



- 優化:在當前結點的 $next [i]$ 為空時,直接將其賦值為等價關係的 $next [i]$[①];否則,將當前結點的 $next [i]$ 的等價關係指向①
- 注意:根結點需要特殊處理,兩種情況都賦值為 root 自身 [②]
- [PS]
- 只有 root 的 $fail$ 指向 NULL
- 銷毀時需要判斷:結點是否為字典樹原生,否則重複 free 可能引發錯誤
- AC 優化使用的結點對應了原生結點
DAT [+AC 自動機]#






- 【一】先根據輸入的單詞們,建立 Trie
- 為了方便,基於 Trie 來實現 DAT
- $cnt$:記錄字典樹的結點數
- 使用了內聯函數,參考C 中關鍵字 inline 用法解析——CSDN
- 【二】將 Trie 轉換為 DAT
- 0] 若該結點成詞,更新 $check$ 為負
- 1] 依次標記子結點的 $check$
- 2] 依次標記子結點的 $base$
- [PS]
- 記錄最大下標
- 結點下標從 1 開始,$base$ 值從 1 開始
- $base$ 值的確定方式有很多,這裡採用的暴力方式
- ⭐ 通過下列信息($index\ |\ base\ |\ check$),即可轉換出字典樹信息
-

- 轉換步驟
-

- ① 先畫出根結點 $index=1$,找 $|check|=index$ 的三元組對應下標,即根結點的子結點下標
- ② 再依次找出子結點的子結點們的下標,進而畫出整棵字典樹的結構
- ③ 最後,根據父結點的 $base$ 值和子結點的編號之差,得到邊對應的字符信息
- [PS]$check$ 值為負→成詞
-
- 👉 雙數組非常方便輸出到文件中,再進行機器之間的共享,即共享 DAT
-
- 比較上面字典樹信息對應的 Trie 和 DAT 實際空間大小
-

- DAT 的壓縮效率約 25 倍❗
- 可嘗試利用真實數據集,測試 DAT 的壓縮效率
-
- [PS] 實現了帶等級的日誌信息系統
- 【三】增加 $fail$ 指針,將 DAT 轉換為基於 AC 自動機的 DAT
- 邏輯不變,代碼實現上注意
- 該結點有第 $i$ 個子結點 👉 該子結點編號對應的 $check$ 值指向自己的編號
- 無需使用路徑壓縮,本身就沒有可利用的 “廢物”
- 邏輯不變,代碼實現上注意
隨堂練習#
HZOJ-282:最大異或對 [Trie]#

樣例輸入
3
1 2 3
樣例輸出
3
- 思路
- 【思考】如何使異或結果盡可能大
- 參與異或運算的兩個數字,二進制表示的每一位盡可能不同
- 【問題轉換】
- 確定一個數字
- 找從高位到低位盡可能不同的另外一個數字 [位置越高權重越大]
- 即找到最大異或對
- 【實現步驟】使用字典樹
- ① 把每個數字看成一個二進制串,插入到字典樹中
- ② 采用貪心的策略,遍歷每個數字,找其對應異或值最大的另一個數字
- ③ 最終得到最大的異或值
- 【思考】如何使異或結果盡可能大
- 代碼


- ⭐亮點很多:直接開辟所有結點空間、順序使用結點空間;擅用位運算;貪心遍歷,邊查詢邊插入
- 結構定義
- 根據題意,最多需要 $31\times 10000$ 個結點,直接開辟好
- 有符號 int 型的有效位為定長 $31$ 位,所以不需要成詞的 $flag$
- 結構操作
- 從高位到低位插入數字的每一位
- 利用邏輯歸一化將有效位轉換為 1,作 $next$ 數組的下標用 [只有 0、1]
- 貪心遍歷
- 查詢時不需要和自己異或,所以查詢完再插入到字典樹
- 當某一位可以異或得 1,擅用位或運算加到答案裡
伴隨編程:字符串統計 [AC]#
【預習】數據結構(C++ 版)

樣例輸入
2
ab
bca
abcabc
樣例輸出
0: 2
1: 1
- 思路
- 多模匹配問題 [AC 自動機裸題]
- 關鍵
- ① 使用解題套路版代碼實現:直接開辟大數組
- ② 維護每一個單詞的計數量:使用幼兒園必知必會的指針技巧
- 注意:輸入數據中給的模式串中有可能重複
- 代碼



- [考驗代碼功底]
- 2 tricks ⭐
- ① 開辟大數組,用下標代表結點
- 數組大小 [結點數量]:最多 $1000\times 20$
- 空結點用 0 表示,記錄下一可用結點編號
- 使用下標時,注意代碼實現思維的轉換
- ② 利用指針綁定模式串與答案,並固定答案的順序,可實時更新
- 針對模式串重複可能,$ans$ 數組也使用 int * 類型,相同模式串的答案可指向同一地址
- 匹配時,操作指針地址上的值即可
- ① 開辟大數組,用下標代表結點
附加知識點#
- 字典樹的本質:字典數據的另外一種表現形式,等價於一本字典
- AC 自動機的本質:狀態機
- 在實際應用中,AC 自動機不如字典樹暴力匹配廣泛 [在開發效率和執行效率中的平衡]
- DFA、NFA 是編譯原理的知識
- 主要區別:DFA 速度更快,NFA 消耗內存更少
- 參考Difference between DFA and NFA——Stechies
Tips#
- 建議:多看幾本基本的算法書、數論基礎書,多接觸離散型數學思維
- 錯誤式學習:學習什麼是錯的,減少錯誤的概率
- 得道者多助,失道者寡助;萬物都有成熟的時令;不積硅步,無以至千里;不積小流,無以成江海
- 寄語:以吾之矛,武裝汝身