5 String Matching Algorithms (Part 2): Trie, AC, DAT

Multi-pattern matching problem, data structures related to string matching

Course Content#

Multi-pattern Matching Problem

The problem of matching multiple pattern strings, the conventional approach is as follows:

Step1: For multiple pattern strings, build a trie
Step2: Align and match with each character of the text string, simulating the process of brute-force matching

Trie#

Also known as a prefix tree or a word search tree, as the name suggests

Understanding through Diagrams#

Consider the meaning of the tree: nodes represent sets, edges represent relationships
The root node can be understood as the entire dictionary, with words starting with 'a' placed in the first subtree, words starting with 'c' in the second subtree, and so on
- Red nodes represent words formed by the letters traversed from the root node to the current node
When an edge representing a certain letter exists [pointing to a node], it indicates the existence of a set of words with the previous letters as prefixes
[PS] Also known as a prefix tree: each string is inserted into this tree structure in the order of prefixes

Common Scenarios#

① Word Search
- Determine whether a certain letter exists based on whether the edge representing that letter points to a node, thus searching for a word
② String Sorting
- By performing a depth-first traversal of a trie, output strings when encountering word markers, achieving ordered output of strings
- Time complexity: $O(n)$, no string size comparison
③ Multi-pattern Matching
- A trie can represent multiple pattern strings, traversing each character of the text string and matching the strings in the trie sequentially to complete multi-pattern matching
- However, this method is essentially a brute-force matching approach under multi-pattern matching

Thoughts on Brute-force Matching#

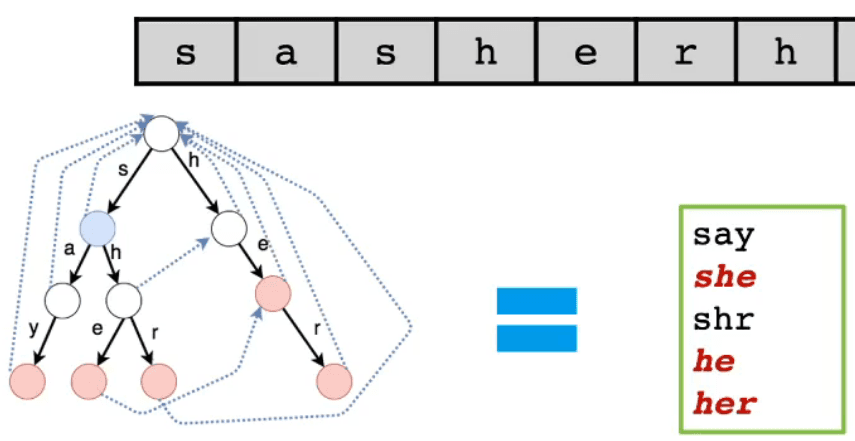
First, consider the brute-force matching process
- After successfully matching "she" in the text string using the trie, the trie moves down one level to try to match the next character 'r' in the text string
- But at this point, there are no nodes below the trie, resulting in a match failure
- The text string pointer backtracks to 'h', and the trie pointer returns to the root node to continue matching, then successfully matches "her"
There is a clear repeated matching process in the above
- After successfully matching "she", it is actually equivalent to successfully matching "he"
- Therefore, when the text string pointer moves one position forward, it should actually be able to successfully match "her"
This includes an equivalence matching relationship [see the red line in the diagram below]
- When there are no matching nodes below the trie, we can also check if we can match through the equivalence matching relationship
- ❗ Can we speed up the matching process through the equivalence matching relationship? The AC automaton provides the answer 👇

AC Automaton#

The idea of a state machine, solving the efficiency problem of multi-pattern matching
AC = Trie + fail [equivalence relationship]

Establishing Equivalence Matching Relationships#

Speeding up the matching process

① For each child node, its default equivalence matching relationship is the root node
② When establishing the equivalence matching relationship for child nodes, it will leverage the equivalence relationship of the parent node
- If not found, it will look for the equivalence relationship of the grandparent node until it reaches the root node
- ❗ The idea of continuously looking up equivalence relationships is exactly the same as the establishment of the $next$ array in KMP, see: 《Advanced Data Structures》——4 String Matching Algorithms (Part 1)
- For example: When looking for the equivalence matching relationship of 'h' under 's', it will find the equivalence matching relationship based on its parent node 's' [i.e., the root node], and since there happens to be 'h' below the root node, the equivalence matching relationship $A$ is established
Note
- When establishing equivalence matching relationships, ensure that the equivalence matching relationships of the upper nodes of that node have been established, so a level-order traversal method can be used with a queue
- Equivalence matching relationships are usually called $fail$ pointers

Matching Process#

Match characters in the current state, and if matching fails, go to the equivalence matching relationship to match

① State Transition
- For example: "sas", when matching the second 's' fails, it will return to the equivalence matching relationship — the root node, and try to match 's' again; until it successfully matches, or the equivalence matching relationship is empty [i.e., the root node cannot be found]
- [PS] In the program implementation, it is more convenient to set the equivalence matching relationship of the root node to NULL
② Word Extraction
- After matching a word marker, it is also necessary to check the word markers of the equivalence matching relationship
- For example: When successfully matching the word "she" in the text string, it also means successfully matching the word "he" in the equivalence relationship
Consider: At this point, the AC automaton is essentially an NFA [nondeterministic finite automaton]
- [Assume: "she" corresponds to node $P$ in the trie, "he" corresponds to node $Q$ in the trie]
- Property 1: The current state $p$, after input character $c$, cannot determine the next state through a single operation【satisfied】
- Property 2: The current state $p$ does not represent a unique state [it also represents state $q$]【satisfied】
Time complexity: $O(k\times n)$, with a large constant
- Because the number of times jumping up through equivalence relationships during the matching process is not fixed
- Can it be optimized? Based on the idea of path compression, see below

Optimization#

Make the state transition process direct

Consider: During state transitions, can the process of jumping up through equivalence relationships be done in one step?
- The current state is $p$, the left side of the diagram shows the equivalence relationship of $p$ [$fail$]
- In the previous process, the right side of the diagram shows the red arrows →, which need to make intermediate jumps through the $fail$ pointer
- 【Goal】 Achieve one-step transition for the red arrows
Optimization: Waste Utilization ⭐
- In the $next$ array of $p$, $b$ and $c$ originally correspond to empty nodes, which is purely wasteful, so why not use them to point to the corresponding nodes of the equivalence relationship? The same applies to $p'$.
- ❗ Note the transitivity: The edge pointing from $p$ to $c$ can be passed through the edge pointing from $p'$ to $c$ [level-order traversal, the relationship of $p'$ pointing to $c$ has been obtained], so during the optimization process of establishing matching relationships, there is actually no need to jump up based on the $fail$ relationship
At this point, the AC automaton is essentially close to a DFA [deterministic finite automaton]
- Property 1: The current state $p$, after input character $c$, can jump to the next state through a single operation【satisfied】
- Property 2: The current state $p$ only represents a unique state【not satisfied】
  - There still exists an equivalence relationship, but the transition can be done in one step
Time complexity: $O(n)$

Double-Array Trie#

Double-array trie, as the name suggests, uses two arrays to represent a trie

Introduction#

Complete Binary Tree
- The tree structure in logical thinking, the actual storage structure is a segment of continuous array space
- Compared to a regular binary tree: saves a lot of storage space for edges [recording the addresses of left/right children]
- Optimization idea: from recording to calculating, saving space
A trie with n nodes
- Allocates space for $BASE \times n$ edges
- But only uses $n - 1$ of those edges
- Therefore, it wastes $BASE \times n - (n - 1) = (BASE - 1) \times n + 1$ edges of space
👉 Referencing the advantages of complete binary trees, the double-array trie is proposed
- Similarly, it calculates the addresses of child nodes without storing edge information

Base Array#

Stores base values

【Helps parent nodes find child nodes】
$base[i]$: the $i$th node stores the $base$ value
- The index of its $j$th child node equals $base[i] + j$
[PS] The $base$ value can be set arbitrarily, can be negative, can be repeated
Consider: If there is only the $base$ array, the following scenario may occur
❌ Two nodes have child nodes with the same index, i.e., node 11 may correspond to multiple parent nodes [3, 5]
Therefore, it is necessary to ensure that after setting the $base$ value, the calculated child node index does not conflict with already used indices

Check Array#

Records the index of parent nodes

【Paternity test, checking who the parent node of the node is】
$check[i]$: the index of the parent node of the $i$th node
- When the child node index calculated through the $base$ value already has a parent, the $base$ value can be changed
❗ Consider: How to record word nodes
- The $base$ value can be set arbitrarily
- The $check$ value represents an index, which must be non-negative, and can start from 1 [the root node]
- 👉 The sign of the $check$ value can be used to indicate whether it is a word
- [PS] $check[i]=0$ can represent that index i has not been used

Formalization#

$child_j = base[father] + j$
$check[child_j] = \left{\begin{aligned}&father& not a word\&-father& is a word\&0& no parent\end{aligned}\right.$
[PS]
- $child_j$: the index of the $j$th child node, $j$ can correspond to a character information
- $father$: the index of the parent node
- $root = 1$, $check[1] = 0$

Summary#

Two arrays store two important pieces of information of the trie
- ① The tree structure relationship between parent and child nodes [$base$+$check$]
- ② Whether the node is an independent word [$check$]
- Thus saving a lot of storage space for edges
One trie 👉 multiple double arrays, one double array 👉 a complete trie
- At this point, the trie is just a tree structure in logical thinking, and the actual storage is two segments of continuous array space
❗ Offline storage structure
- Very convenient for transmission and restoration
- But dynamic insertion is extremely time-consuming
- In actual use, establish once and use multiple times [for querying]

+ Binary Trie#

As the name suggests, each node has only two branches

A trie for inserting binary strings can insert any information [any information in a computer can be viewed as a binary string]
Extremely space-efficient, but time-consuming
- Reduces width, increases depth
- Essentially: time for space
⭐ Binary Trie + Huffman Coding
- While saving space, maximally reduces search time [reducing depth]

Code Demonstration#

Trie#

The above is the standard data structure code implementation of the trie, for the technical implementation method for problem-solving see below [HZOJ-282]
Structure Definition
- For 26 letters, the node corresponds to store 26 nodes, which can be understood as representing letter information with 26 edges
- Through the $flag$, mark word nodes
Structure Operations
- Inserting a word does not change the address of the root node, so the function return value is void
- If there is a node pointing to a certain index, it indicates that the corresponding letter information exists
⭐ String Sorting
- By using $k$ to indicate the current layer, $s$ to store string information, and placing 0 at the end each time, ready to output the string at any time
- Using recursion for depth-first traversal, the key is to understand $k$

AC Automaton#

Regular Version#

The $next$ array is not fully utilized

Build the Trie 👉 Establish equivalence matching relationships [queue, $fail$] 👉 Matching [state transition, word extraction]
Note
- The operation of jumping up based on equivalence relationships occurs not only during the establishment and use of matching but also during the word extraction process
- The while loop for establishing and using equivalence matching relationships is time-consuming and can be optimized
[Consider: Establishing equivalence relationships] The equivalence matching relationship of the child nodes of the root node must point to the root node
- If line 64 uses if, it needs to consider the case where $p$ is the root in the first loop
- $c$ is a child node of the root, $k$ is directly NULL, and in line 60 it will directly exit the while loop, in line 62 $k$ is assigned to root, but if line 64 uses if, root->next[i] must hold true, because it is the child node of the root itself
- Here, the child nodes of the root node can be considered uniformly, but in the optimized version, they still need to be handled separately

Optimized Version#

Fully utilize the $next$ array, both the establishment and matching processes have been optimized

Optimization: When the current node's $next[i]$ is empty, directly assign it to the equivalence relationship's $next[i]$ [①]; otherwise, point the current node's $next[i]$ equivalence relationship to ①
- Note: The root node needs special handling, both cases are assigned to the root itself [②]
[PS]
- Only the root's $fail$ points to NULL
- When destroying, it is necessary to check whether the node is a native trie node, otherwise, repeated free may cause errors
  - The nodes used in AC optimization correspond to the native nodes

DAT [+AC Automaton]#

【1】 First, based on the input words, build the Trie
- For convenience, implement DAT based on Trie
- $cnt$: records the number of nodes in the trie
- Used inline functions, refer to C inline keyword usage analysis——CSDN
【2】 Convert the Trie to DAT
- 0] If the node is a word, update $check$ to negative
- 1] Sequentially mark the child nodes' $check$
- 2] Sequentially mark the child nodes' $base$
- [PS]
  - Record the maximum index
  - Node indices start from 1, $base$ values start from 1
  - There are many ways to determine the $base$ value, here a brute-force method is used
- ⭐ Through the following information ($index\ |\ base\ |\ check$), the trie information can be converted
  - Conversion Steps
    - ① First draw the root node $index=1$, find the triplet corresponding index where $|check|=index$, which is the index of the root node's child nodes
    - ② Then sequentially find the indices of the child nodes' children, thus drawing the entire structure of the trie
    - ③ Finally, based on the difference between the parent node's $base$ value and the child node's index, obtain the character information corresponding to the edge
    - [PS] $check$ value is negative → is a word
  - 👉 The double array is very convenient for outputting to files, and then sharing between machines, i.e., sharing DAT
- Compare the actual space size of the trie information corresponding to the above trie and DAT
  - The compression efficiency of DAT is about 25 times ❗
  - You can try using real datasets to test the compression efficiency of DAT
- [PS] Implemented a logging information system with levels
【3】 Add the $fail$ pointer, converting DAT to DAT based on the AC automaton
- The logic remains unchanged, pay attention to the code implementation
  - If the node has the $i$th child node 👉 the $check$ value corresponding to that child node points to its own index
- No need to use path compression, as there are no "waste" to utilize

In-Class Exercise#

HZOJ-282: Maximum XOR Pair [Trie]#

Sample Input

3
1 2 3

Sample Output

Thought Process
- 【Consider】 How to make the XOR result as large as possible
  - The two numbers participating in the XOR operation should have binary representations that differ as much as possible in each bit
- 【Problem Transformation】
  - Fix one number
  - Find another number that is as different as possible from high bits to low bits [the higher the position, the greater the weight]
  - That is, find the maximum XOR pair
- 【Implementation Steps】 Use the trie
  - ① Treat each number as a binary string and insert it into the trie
  - ② Use a greedy strategy to traverse each number and find the corresponding number that maximizes the XOR value
  - ③ Finally obtain the maximum XOR value
Code
- ⭐ Many highlights: directly allocate space for all nodes, sequentially use node space; adept use of bit operations; greedy traversal, querying while inserting
- Structure Definition
  - According to the problem, a maximum of $31\times 10000$ nodes are needed, directly allocate
  - The effective bits of signed int type are fixed-length $31$ bits, so no need for a word $flag$
- Structure Operations
  - Insert each bit of the number from high to low
  - Use logical normalization to convert effective bits to 1, serving as indices for the $next$ array [only 0, 1]
- Greedy Traversal
  - During querying, there is no need to XOR with itself, so insert into the trie after querying
  - When a bit can yield 1 in XOR, adeptly use bitwise OR to add to the answer

Accompanying Programming: String Statistics [AC]#

【Preview】 Data Structures (C++ Version)

Sample Input

2
ab
bca
abcabc

Sample Output

0: 2
1: 1

Thought Process
- Multi-pattern matching problem [AC automaton bare question]
- Key
  - ① Use the problem-solving template code: directly allocate a large array
  - ② Maintain the count for each word: use pointer techniques that are essential for kindergarten
- Note: The pattern strings given in the input data may be repeated
Code
- [Tests coding skills]
- 2 tricks ⭐
  - ① Allocate a large array, using indices to represent nodes
    - Array size [number of nodes]: at most $1000\times 20$
    - Empty nodes are represented by 0, recording the next available node index
    - When using indices, pay attention to the conversion of thought in code implementation
  - ② Use pointers to bind pattern strings with answers, and fix the order of answers, allowing real-time updates
    - For possible repeated pattern strings, the $ans$ array also uses int* type, so the answers for the same pattern string can point to the same address
    - During matching, operate on the values at the pointer addresses

Additional Knowledge Points#

The essence of the trie: another representation of dictionary data, equivalent to a dictionary
The essence of the AC automaton: a state machine
In practical applications, the AC automaton is not as widely used as the brute-force matching of tries [balancing development efficiency and execution efficiency]
DFA and NFA are knowledge from compiler principles
- Main difference: DFA is faster, NFA consumes less memory
- Refer to Difference between DFA and NFA——Stechies

Tips#

Recommendation: Read several basic algorithm books, foundational number theory books, and get familiar with discrete mathematics thinking
Learning from mistakes: Understand what is wrong to reduce the probability of errors
Those who follow the path will have more help; those who stray will have less help; everything has its season; without accumulating small steps, one cannot reach a thousand miles; without accumulating small streams, one cannot form rivers and seas
Message: Arm yourself with my spear