4 字串匹配演算法（上）：BF、KMP、SUNDAY、SHIFT-AND、Hash

一些經典、絕倫的單模匹配相關算法

課程內容#

相關定義

單模匹配問題：在文本串 $s$ 中查找某個模式串 $t$ 是否出現過

多模匹配問題：查找多個模式串 $t$

文本串 / 母串：被查找串 $s$

模式串：待查找串 $t$

文本串長度為 $m$，模式串長度為 $n$

暴力匹配法#

所有字符串匹配算法的基石

思想#

依次對齊模式串和文本串的每一位，直到完全匹配
其思想是理解所有匹配算法的基礎：不漏的找到答案
- 而其他算法優化的核心就是不重，減少重複的、不可能匹配成功的嘗試
時間複雜度：$O (m\times n)$

引發思考#

第一次失配時，暴力匹配是怎麼處理的？

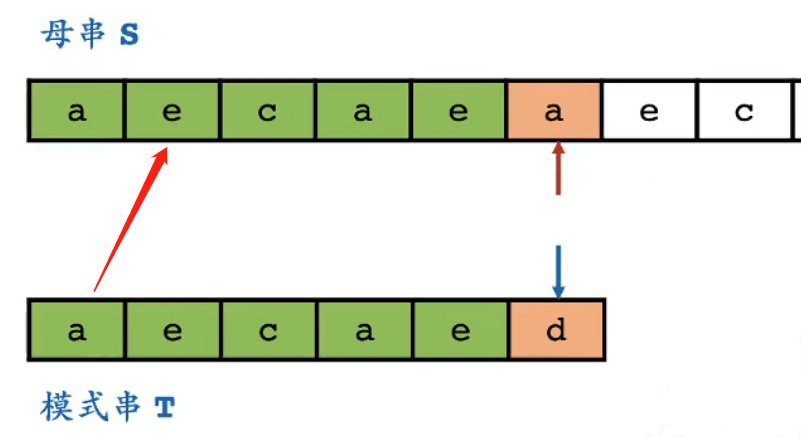
它會用模式串第一位與母串的第二位進行匹配
而如果匹配成功，意味著模式串第一位與文本串第二位相等
- 因為已知模式串的第二位與文本串的第二位是匹配成功的
- 那麼必然存在，模式串的第二位與第一位相等
模式串的第二位與第一位是否相等，其實在拿到模式串時就可以知道
對於上圖，完全沒有必要嘗試用模式串第 1 位與母串第 2 位進行匹配
- 它們肯定不匹配
是否可以跳過肯定不匹配的位置，KMP 算法有自己的想法

KMP#

狀態機思想、自身結構重複展開概念

思考過程#

接上，關注 A、B、C 位置

【假設】在黑色陰影處失配時，模式串 $t$ 往後移動④的大小，此時文本串 $s$ 的②和模式串 $t$ 的①匹配成功的情況
【關鍵】第③部分：其左邊界決定 $t$ 往後移動的距離 [同第①部分右邊界]
【A】在這一豎列上，一定存在②=③=①，②緊挨著失配位置 👉 ③也緊挨著失配位置
【B】③實際是 $t$ 的後綴，①是 $t$ 的前綴 👉 ③等於 $t$ 的某個前綴
【C】為了保證不漏匹配，④應該盡可能的小 👉 ③應該盡可能的大
【結論】綜上所述，通過③可以加速匹配過程，而③是緊挨失配位置的、$t$的最長前綴

問題轉換#

預先得到失配時對應的③的大小，也是①的大小

尋找模式串的①和③，用①後面的綠色字符去匹配②後面失配位置的橙色字符
要考慮模式串的每一位：因為失配的位置可能是模式串的每一位
模式串是預先知道的；文本串是不知道的、不可控的
👉 模式串的 $next$ 數組

next 數組#

$next [i]$：當 $i$ 位置匹配成功，但 $i+1$ 位置失配時使用，作為模式串下一次嘗試匹配的偏移
狀態定義：以 $i$ 位置結尾的後綴中，可以匹配的最長前綴的下標 [右邊界]
- 只針對模式串
轉移公式：看圖理解，關注圖中①②處
- $next[i+1]=\left{\begin{aligned}&next[i]+1&t[i+1]=t[next[i]+1]\&next[next[i]]+1&t[i+1]\neq t[next[i]+1]\ &&\ t[i+1]=t[next[next[i]]+1]\&next[next[next[...[i]]]]+1&until\ equal\ or\ the\ end\end{aligned}\right.$
- 先看第二、三行，判斷①
  - 如果 $t [i+1]=t [next [i]+1]$，則 $i+1$ 對應的最長前綴為 $next [i]+1$
  - 否則，將 $t$ 再向右移動盡可能短的距離 [類似上文思考過程中的④]，也就是找到子串 $t [0\to j]$ 中，以 $j$ 結尾的後綴中，對應的最大前綴 [這就是 $next$ 數組定義]
- 觀察第一、二行，判斷②
  - 如果 $t [i+1]=t [next [j]+1]$，則 $i+1$ 對應的最長前綴為 $next [j]+1$，其中 $j=next [i]$
  - 否則，繼續將 $t$ 右移，判斷③④... 直到滿足等於關係，或者 $t$ 不能再右移
涉及動態規劃的思想，可跳轉《面試筆試算法下》——1 從遞推到動態規劃（上）
練習理解
- 定義虛擬位置：-1 [當匹配不到任何前綴時，值為 - 1]
- 練習 1
- 練習 2
- 答案：-1、-1、0、-1、0、1、2、3、4、5、6、1
[PS] 參考KMP 算法詳解——CSDN
- 文中 $next$ 數組定義為：前綴和後綴的最大公共長度[不包括字符串本身，否則最大長度始終是字符串本身]
- 可見 $next$ 數組的定義不唯一
- 自身結構重複展開概念，求 $next$ 數組時就有這個思想

匹配過程#

依次遍歷文本串 $s$ 的每一位
從模式串 $t$ 起始位開始匹配
1. 如果文本串 $s$ 的當前位置與模式串 $t$ 的當前位置相等，則匹配模式串 $t$ 的下一位
2. 否則，根據 $next$ 數組不斷前移模式串 $t$ 的嘗試匹配位置，直到相等條件成立，匹配模式串 $t$ 的下一位；或者不能再前移，匹配文本串 $s$ 的下一位
當成功匹配到模式串 $t$ 的結尾時，輸出文本串 $s$ 對應匹配的位置；或者沒有找到

小結#

理解模式串中的第③部分的重要性 [見思考過程]
- 加快匹配速度的核心，避免掉大量無用的匹配嘗試
保證不漏的核心：第③部分匹配到的是模式串的最長前綴
可以從狀態機的角度理解，見代碼演示 —— 狀態機版 KMP
時間複雜度：$O (m + n)$
[PS] KMP 還存在一些優化方法

SUNDAY#

先找腚，再找頭

模擬操作#

直接模擬一遍如下情況

① 當發生失配時，觀察模式串 $t$ 末尾對應母串 $s$ 位置的后一位e——黃金對齊點位
- [注意] 不是觀察失配位置后一位 < 不要被圖誤解 >
② 在模式串 $t$ 中，從後向前找第一個e 的位置
- 在倒數第 2 位找到 e
③ 倒數第 2 位意味著，模式串 $t$ 對母串 $s$ 的嘗試匹配位置向右移動正數 2 位，然後重頭嘗試匹配母串 $s$
- [個人理解] 如果該右移要匹配成功，e 位置必須對齊，因為總會經過 e；找第一個 e，是為了不漏答案
④ 上圖仍然發生失配，此時再在模式串 $t$ 中，從後往前找第一個 a，再對齊，匹配... 直到成功匹配，或者匹配結束
[PS] 如果找不到黃金對齊點位對應的字符，則右移的偏移量為整個模式串 $t$ 的長度 + 1

流程#

預處理每一個字符在模式串中最後一次出現的位置
模擬暴力匹配算法過程，失配的時候，文本串指針根據上述預處理信息，向後移動相應位，然後重新匹配
最終，匹配成功返回下標，或者找不到

小結#

核心：理解黃金對齊點位 [詳見模擬操作]
- 如果匹配成功，其一定會出現在模式串中
- 其應該和模式串中最後一個出現該字符的位置對齊
右移操作：所找字符出現在模式串的倒數第幾位，就將文本串指針右移幾位
最快時間複雜度：$O (m /n)$
- 對應場景：要尋找的黃金對齊點位字符，在模式串中沒有找到，文本串指針將向後移動整個模式串長度 $n + 1$ 的距離
[PS]
- 最壞時間複雜度：$O (m\times n)$，但此種情況對應的字符串一般沒有實際意義
- 使用場景：解決 “一篇文章中查找一個單詞” 等簡單的單模匹配問題 < 工業中很常用 >
- 對比 KMP
  - SUNDAY 更好理解與實現
  - 但 KMP 算法的思維方式更高級，應該學習 [狀態機]

SHIFT-AND#

非常優美的小眾算法，考察想象力
狀態機思想：NFA，非確定性有窮狀態自動機

編碼數組 d#

⭐將模式串轉換為一種編碼，轉換完後匹配問題就和模式串沒有一毛錢關係了

從第 0 位開始，依次讀取模式串 t 的每一位
當在第 0 位出現 'a' 字符時，將 $d$ 數組中下標為 'a' 的元素第 0 位置 1
當在第 1 位出現 'e' 字符時，將 $d$ 數組中下標為 'e' 的元素第 1 位置 1
以此類推，得到 $d$ 數組
[PS]
- $d$ 數組下標可以對應字符的 ASCII 碼
- $d$ 數組元素可以存儲 int 類型 [32 位]、long long 類型或者自定義類型，這決定可匹配的最長模式串長度
- 注意字符串序和 $d$ 數組元素的數字序，第 0 位字符對應後者的低位

狀態信息 p#

理解狀態定義，感受轉移狀態

狀態定義：$p_i$
- 在 $p_i$ 的二進制表示中，如果第 $j$ 位為 1，則代表以文本串 $s [i]$ 結尾時，可以成功匹配模式串的前 $j$ 位
- 圖解，對照上述定義與下面的三對圓圈
  - 紅色：$p_4$ 代表以文本串 $s [4]$結尾，為現在的匹配條件
  - 橙色：$p_4$ 的第 2 位為 1，代表模式串 $t$ 的前 2 位可以滿足上面匹配條件，即 $t [0\to 1]$ 與 $s [3\to 4]$ 匹配
  - 綠色：$p_4$ 的第 5 位為 1，代表模式串 $t$ 的前 5 位可以滿足上面匹配條件，即 $t [0\to 4]$ 與 $s [0\to 4]$ 匹配
  - [PS]
    - $p$ 的二進制長度取決於使用什麼數據類型，同 $d$ 數組元素，如 int：32 位
    - 暫不關注 $p_4$ 是如何來的，稍後看轉移過程
- ⭐由此可見
  - $p$ 中同時存儲著多個匹配結果的信息❗
  - 當 $p_i$ 的第 $n$ 位為 1 時，匹配成功，即
    - $p_i\ &\ (1\ <<\ (n-1))=1$
    - 匹配位置為：$i-n+1$
轉移過程：$p_i=(p_{i-1}\ <<\ 1\ |\ 1)\ &\ d [s [i]]$
- ⭐關鍵公式⭐
- 此時已完全拋開模式串 $t$，通過 $p$ 的上一个狀態和 $d$ 數組，即可得此時的 $p$ 值
- 原理分析，對照關鍵公式和下圖的①②
  - 假設已知 $p_3$，當前可以匹配 $s [2\to 3]$ 和 $s [0\to 3]$
  - ①左移 1 位+或 1 運算，得到過渡狀態 $p_4^{'}$
    - 左移 1 位：試圖在前一個匹配基礎上，吞併 $s [4]$，即匹配 $s [2\to 4]$ 和 $s [0\to 4]$
      - 匹配成功的條件在於後面的【與運算】
      - [注意] 左移操作在圖中表現為右移，因為數字順序是低位在前
    - 或 1 運算：留一個單獨匹配 $s [4]$ 的機會，匹配成功代表匹配這一個字符
  - ②與運算
    - 上面兩個操作都只是嘗試匹配，而真正成功與否取決於 $d [s_4]$ 的表現
    - 如果第 $j$ 位上與運算的結果為 1，則代表成功匹配 $s [4-j+1\to 4]$ 與 $t [0\to j-1]$
      - 如 $p_4 [2]=1$、$p_4 [5]=1$，匹配結果即狀態定義部分的圖解
[PS]
- $p$ 的初始值為 0，$p$ 實際上是一個非確定性有窮狀態自動機
- 習慣衝突：一般數字順序右側是低位，但在圖中 $p$ 的左側是低位；二進制數字最低位是 1，字符串最低位是 0；$d$ 數組元素是數字，所以應該對應數字順序，但上圖是為了體現與模式串的對應位置關係，用的字符串順序
- 準確理解 $p$ 的含義：上一次成功匹配 4 位，下一次才有可能成功匹配 5 位
- 對於多於 64 位的字符串匹配問題，需要自己創建數據類型
  - 支持左移、或、與運算即可
  - 再對應修改編碼數組 $d$ 和狀態信息 $p$ 的類型

小結#

① 編碼數組 $d$：將模式串中每一種字符出現的位置，轉換成相應的二進制編碼
② 狀態信息 $p$：通過關鍵公式 $p_i=(p_{i-1}\ <<\ 1\ |\ 1)\ &\ d [s [i]]$ 轉移狀態
時間複雜度：$O (m)$
- 完全不需要對模式串來回倒
- 但是嚴謹來說，不是純 $O (m)$，這和計算機的數據表示能力有關
❗ 可以解決正則表達式匹配問題
- 例如：$(a|b|c)&(c|d)&e&(f|a|b)$
- ① 將上述模式串轉換為編碼數組 $d$
  - 對於 $d$ 數組的每一縱列可以有多位，置 1
  - 即模式串的每一位可以讓多個【$d$ 數組的元素】的對應二進制位，置為 1
- ② 之後就與模式串無關了，根據 $d$ 數組和關鍵公式解決問題
- [PS] 這裡可以看出模式串之所以叫模式串，是因為它不只是指字符串，還可以是正則表達式（也可以看作一種有相關性的多模式）

代碼演示#

暴力匹配法#

兩種版本，學習簡潔版的技巧，靈活運用 $flag$
分別遍歷文本串和模式串，逐位判等，若失配，將文本串指針右移一位
該思想是所有字符串匹配算法的基礎

KMP#

2 種編程方式，後者更接近於算法的本質思想

① 普通編碼：直接獲得 $next$ 數組，再使用 $next$ 數組做失配偏移
- 預處理 $next$ 數組→遍歷文本串每一位→匹配模式串 [利用 $next$ 數組]
- ❗ 觀察：獲取 $next$ 數組的過程和匹配文本串的過程非常相似，基於狀態機的思想，可將兩部分整合
② 高級編程：基於狀態機的思想，將獲取 $next$ 值的過程轉化成狀態的改變過程
- 抽象化了一個狀態機模型：$j$ 所指向的就是狀態機的位置，$getNext$ 方法相當於根據輸入字符，進行狀態跳轉，實際上就是改變 $j$ 的值
- 更接近 KMP 本質的思維方式
PS：應該在匹配成功了返回 $i-n+1$ 前也對 $next$ 數組進行 free

SUNDAY#

❗ 注意 256 的含義：用來記錄每種字符在模式串中的位置
預處理 $offset$ 數組的過程：先初始化為都沒有出現的情況，$n+1$ 表示文本串指針可以直接右移一個模式串長度 + 1 的距離；在預處理過程中，後面相同字符出現的位置會覆蓋前面的，正合 SUNDAY 意
$s [i + n]$：黃金對齊點位對應的字符
$i + n <= m$：合理地利用了 $n$、$m$ 變量，表示文本串還夠模式串匹配
相比 KMP，SUNDAY 更好理解，代碼更好實現 [解決簡單單模匹配問題的不二選擇]

SHIFT-AND#

⭐ 思想優美，代碼簡單
注意
- 與數字有關的 $d$ 數組元素和狀態 $p$，最低位為 1；而字符串對應為 0
- 但轉移過程是數字之間的運算，所以不用顧慮位置是否對齊

隨堂練習#

——Hash——#

常用的解題套路

HZOJ-275：兔子與兔子#

樣例輸入

aabbaabb
3
1 3 5 7
1 3 6 8
1 2 1 2

樣例輸出

Yes
No
Yes

思路
- 注意：查詢次數特別多，查詢區間非常大，暴力匹配一定超時
- 如何快速比較？👉 哈希匹配算法
  - 通過哈希操作將字符串用數字 <哈希值> 表示
  - 如果兩個字符串對應的哈希值不同，兩個字符串一定不相等
    - 這樣就剔除了大部分不相等的情況，而不需要再按位比較了
  - 否則，再通過暴力匹配驗證字符串是否相等
    - 如果兩個字符串相等，一次匹配就能成功
  - [PS]
    - 長字符串直接對應的哈希值可能太大，所以一般通過取余操作縮小哈希值
    - 餘數不一樣 👉 字符串肯定不一樣
- 設計哈希函數 [字符串 -> 哈希值]
  - $H=(\sum_{k=0}^{n-1}{C_k\times base^k})%P$
  - $n$：字符串 $s$ 的長度
  - $C_k$：第 $k$ 位字符對應的 ASCII 碼值
  - $base$：位權 [素數]
  - $P$：模數 [素數]
  - [PS] 字符在計算機底層是用二進制數字存儲的
- ⭐本題中一個子串 $s [j\to i]$ 的哈希值 $H_{j\to i}$
  - 根據字符串與哈希值的關係，可以預先處理得到基於哈希的前綴和數組
    - $HS_i=(\sum_{k=0}^{i}{C_k\times base^k})%P$
  - 從而得到子串 $s [j\to i]$ 基於哈希的區間和為
    - $HS_{j\to i}=(\sum_{k=j}^{i}{C_k\times base^k})%P$
  - 但是對於子串的哈希值，不應該包含子串在字符串中的位置信息 $j$、$i$，即乘數因子應該從 $base^0$ 開始
  - 所以，需要將區間和 $HS_{j\to i}$ 除以 $base^j$，但是對於取余運算，不能直接做除法，而需要借助逆元
  - 最終子串 $s [j\to i]$ 的哈希值 $H_{j\to i}$ 轉換為
    - $H_{j\to i}=HS_{j\to i}\times(base^j)^{-1}%P=(HS_i-HS_{j-1})\times(base^j)^{-1}%P$
    - $(base^j)^{-1}$：$base^j$ 的逆元
    - 逆元的快速求解請跳轉到：快速求 [模] 逆元
- 解題方式①
  - 1. 在文本串上，預先處理得到每一位基於哈希的前綴和，方便一會求區間和
  - 1. 通過區間和與逆元，求得某子串 $s [i\to j]$ 的哈希值：
    - $H_{j\to i}=HS_{j\to i}\times(base^j)^{-1}%P$
  - 1. 比較兩個子串的哈希值
    - 如果不相等，子串一定不相同
    - 否則，再用暴力匹配驗證是否相同
  - ❗ 兩個子串不相同，但其哈希值相等的可能性為 $1/P$
- 解題方式②
  - 基於方式①，設計兩個哈希函數，對應 $P$、$base$ 不同
  - 比較兩個子串對應的兩個哈希值
    - 都相等時，認定兩個子串相同
    - 否則，一定不相同
  - ❗ 兩個子串不相同，但其哈希值相等的可能性為 $1/(P_1\times P_2)$
    - 出錯的概率極低，其實有很多算法都是概率性算法
代碼
- 方式①：哈希匹配 + 暴力匹配
- ①$P$ 值必須為素數，否則部分逆元沒有意義，對應求出來的哈希值不正確
  - 這會導致相同的子串也對應不同的哈希值
  - 逆元存在的充分必要條件：互質
- ② 需要使用 long long 類型，中間過程的數值可能非常大
  - 這會增大不同子串對應哈希值相同的概率，增加耗時 [暴力匹配]
- [PS]
  - 時刻記得取余，防止數字超過表示範圍，即使是 long long
  - 注意保證哈希值為正
    - 基於哈希的前綴和數組 $H$ 不是單調遞增的，因為求和時都有取余操作
  - $P$ 值過小可能導致超時，暴力匹配次數過多
- 方式②：哈希匹配 * 2
- 注意：兩個逆元數組分開初始化，保證初始化完全 [遍歷的範圍不一樣]
  - 或者使用相同的 $P$ 和不同的 $base$，可以一起初始化
- [PS] 為了保險，可以再加入暴力匹配驗證

快速求 [模] 逆元#

⭐推導過程

目標：求解 $x\times x^{-1}\equiv1\ (mod\ P)$ 中的 $x^{-1}$
- [PS] 只考慮 $x<P$ 的情況，因為所有大於 $P$ 的 $x$ 都可以通過取余轉換為小於 $P$ 的 $x$
令：$P\ %\ x=r,P\ /\ x=k$
則：
- $\begin{aligned}P&=kx+r\kx+r&\equiv0\ (mod\ P)\kx(x^{-1}r^{-1})+r(x^{-1}r^{-1})&\equiv0\ (mod\ P)\kr^{-1}+x^{-1}&\equiv0\ (mod\ P)\x^{-1}&\equiv-kr^{-1}\ (mod\ P)\\end{aligned}$
最終將求 $x^{-1}$ 的問題，轉換為求 $r^{-1}$ 的問題
- 而 $r$ 是模 $x$ 的餘數，所以 $r$ 一定比 $x$ 更小
一個規模較大的問題 👉 一個規模較小的問題 [遞推]
為保證逆元為正，再做一次處理
- $x^{-1}_{+}=(-kr^{-1}\ %\ P+P)\ %\ P$
[PS]
- 模逆元：逆元存在的充分必要條件是 $p$ 和 $x$ 互質
- 求逆元的方法很多，參考逆元知識普及 (掃盲篇)——cnblogs

代碼

不管模數為幾，1 的逆元就是 1 [初始化]
輸出結果
- 可自行驗證：原數與逆元相乘取余為 1

附加知識點#

KMP、SHIFT-AND 的本質思想：狀態機 <在編譯原理中會學到的知識>
SUNDAY 算法在生活中很常用，Hash 匹配算法在解題中常用
DFA、NFA 是編譯原理的知識
- 主要區別：DFA 速度更快，NFA 消耗內存更少
- 參考Difference between DFA and NFA——Stechies

Tips#

上 C++ 之前，一定先刷完預修課
成為算法領域裡的內行，關鍵在提高自己的審美能力
生氣是無能的表現，幹正事！一步一步變好，不求一蹴而就