4 String Matching Algorithms (Part 1): BF, KMP, SUNDAY, SHIFT-AND, Hash

Some classic and unparalleled algorithms related to single pattern matching

Course Content#

Related Definitions

Single Pattern Matching Problem: Finding whether a certain pattern string $t$ appears in the text string $s$

Multi-pattern Matching Problem: Finding multiple pattern strings $t$

Text String/Main String: The string being searched $s$

Pattern String: The string to be searched $t$

The length of the text string is $m$, and the length of the pattern string is $n$

Brute Force Matching Method#

The cornerstone of all string matching algorithms

Idea#

Align each position of the pattern string and the text string sequentially until a complete match is found
The idea is the foundation for understanding all matching algorithms: to find the answer without missing anything
- The core of other algorithm optimizations is to avoid redundancy, reducing attempts that cannot match successfully
Time Complexity: $O(m \times n)$

Provoking Thoughts#

How does brute force matching handle the first mismatch?

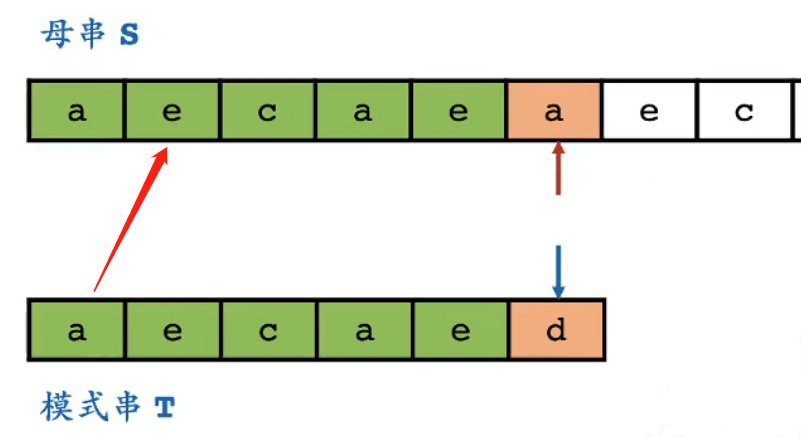
It will match the first position of the pattern string with the second position of the main string
If the match is successful, it means the first position of the pattern string is equal to the second position of the text string
- Since it is known that the second position of the pattern string matches successfully with the second position of the text string
- There must be a situation where the second position of the pattern string is equal to the first position
Whether the second position of the pattern string is equal to the first position can actually be known when obtaining the pattern string
For the above image, there is no need to attempt matching the first position of the pattern string with the second position of the main string
- They definitely do not match
Is it possible to skip positions that definitely do not match? The KMP algorithm has its own ideas.

KMP#

State machine thinking, concept of self-structure repetition expansion

Thought Process#

Continuing, focus on positions A, B, C

[Assume] When a mismatch occurs at the black shadow area, the pattern string $t$ moves forward by the size of ④, at this time the text string $s$'s ② and the pattern string $t$'s ① match successfully
[Key] The third part: its left boundary determines the distance $t$ moves forward [same as the right boundary of the first part]
[A] In this vertical column, there must be ②=③=①, with ② adjacent to the mismatch position 👉 ③ also adjacent to the mismatch position
[B] ③ is actually a suffix of $t$, and ① is a prefix of $t$ 👉 ③ equals some prefix of $t$
[C] To ensure no matches are missed, ④ should be as small as possible 👉 ③ should be as large as possible
[Conclusion] In summary, through ③, the matching process can be accelerated, and ③ is the longest prefix of $t$ that is adjacent to the mismatch position.

Problem Transformation#

Pre-obtain the size of ③ corresponding to the mismatch, which is also the size of ①

Find the ① and ③ of the pattern string, use the green characters after ① to match the orange characters at the mismatch position after ②
Consider each position of the pattern string: because the mismatch position could be any position of the pattern string
The pattern string is known in advance; the text string is unknown and uncontrollable
👉 The $next$ array of the pattern string

Next Array#

$next[i]$: Used when the $i$ position matches successfully, but the $i+1$ position mismatches, as the offset for the next attempt to match the pattern string
State Definition: The index of the longest prefix that can match in the suffix ending at position $i$ [right boundary]
- Only for the pattern string
Transition Formula: Understand by looking at the diagram, focus on positions ① and ② in the diagram
- $next[i+1]=\left{\begin{aligned}&next[i]+1&t[i+1]=t[next[i]+1]\&next[next[i]]+1&t[i+1]\neq t[next[i]+1]\ &&\ t[i+1]=t[next[next[i]]+1]\&next[next[next[...[i]]]]+1&until\ equal\ or\ the\ end\end{aligned}\right.$
- First look at the second and third lines, determine ①
  - If $t[i+1]=t[next[i]+1]$, then the longest prefix corresponding to $i+1$ is $next[i]+1$
  - Otherwise, move $t$ to the right as short as possible [similar to ④ in the thought process above], which is to find the maximum prefix corresponding to the suffix ending at $j$ in the substring $t[0\to j]$ [this is the definition of the $next$ array]
- Observe the first and second lines, determine ②
  - If $t[i+1]=t[next[j]+1]$, then the longest prefix corresponding to $i+1$ is $next[j]+1$, where $j=next[i]$
  - Otherwise, continue to move $t$ to the right, checking ③④... until the equality condition is satisfied, or $t$ can no longer move to the right
Involves the idea of dynamic programming, see "Interview and Written Algorithm Part 2" — 1 From Recursion to Dynamic Programming (Part 1)
Practice Understanding
- Define a virtual position: -1 [when no prefix matches, the value is -1]
- Practice 1
- Practice 2
- Answers: -1, -1, 0, -1, 0, 1, 2, 3, 4, 5, 6, 1
[PS] Reference KMP Algorithm Detailed Explanation — CSDN
- In the text, the $next$ array is defined as: the maximum common length of the prefix and suffix [excluding the string itself, otherwise the maximum length is always the string itself]
- It can be seen that the definition of the $next$ array is not unique
- The concept of self-structure repetition expansion, when seeking the $next$ array, has this idea

Matching Process#

Traverse each position of the text string $s$ sequentially
Start matching from the beginning of the pattern string $t$
1. If the current position of the text string $s$ is equal to the current position of the pattern string $t$, then match the next position of the pattern string $t$
2. Otherwise, based on the $next$ array, continuously move the attempt position of the pattern string $t$ forward until the equality condition is satisfied, match the next position of the pattern string $t$; or cannot move forward anymore, match the next position of the text string $s$
When successfully matching to the end of the pattern string $t$, output the corresponding matching position of the text string $s$; or not found

Summary#

Understand the importance of the third part in the pattern string [see thought process]
- The core to speed up matching, avoiding a large number of useless matching attempts
The core to ensure no matches are missed: the third part matches the longest prefix of the pattern string
Can be understood from the perspective of a state machine, see code demonstration — State Machine Version KMP
Time Complexity: $O(m + n)$
[PS] KMP also has some optimization methods

SUNDAY#

Find the tail first, then find the head

Simulation Operation#

Directly simulate the following situation

① When a mismatch occurs, observe the next position e corresponding to the end of the pattern string $t$ in the main string $s$ — golden alignment point
- [Note] Do not observe the position after the mismatch <don't be misled by the image>
② In the pattern string $t$, find the first position of e from the back
- Found e at the second to last position
③ The second to last position means that the attempt matching position of the pattern string $t$ with the main string $s$ moves forward by 2 positions, then retry matching the main string $s$ from the beginning
- [Personal Understanding] If this right shift is to match successfully, the e position must align, because it will always pass through e; finding the first e is to avoid missing answers
④ The above image still has a mismatch, at this time find the first a in the pattern string $t$ from the back, align it, match... until successfully matched, or the matching ends
[PS] If the character corresponding to the golden alignment point cannot be found, the right shift offset will be the length of the entire pattern string $t$ + 1

Process#

Preprocess the last occurrence position of each character in the pattern string
Simulate the brute force matching algorithm process, when a mismatch occurs, the text string pointer moves back according to the above preprocessing information, then re-matches
Finally, return the index if matched successfully, or not found

Summary#

Core: Understand the golden alignment point [see simulation operation]
- If matching is successful, it must appear in the pattern string
- It should align with the last occurrence position of that character in the pattern string
Right shift operation: The position of the character found in the pattern string from the end determines how many positions to shift the text string pointer to the right
Fastest Time Complexity: $O(m / n)$
- Corresponding scenario: If the character to find the golden alignment point is not found in the pattern string, the text string pointer will move back the entire length of the pattern string $n + 1$.
[PS]
- Worst-case time complexity: $O(m \times n)$, but this scenario generally has no practical significance
- Usage scenario: Solving simple single-pattern matching problems like "finding a word in an article"
- Compared to KMP
  - SUNDAY is easier to understand and implement
  - But the thinking of the KMP algorithm is more advanced and should be learned [State Machine]

SHIFT-AND#

A very elegant niche algorithm that tests imagination
State machine thinking: NFA, Non-deterministic Finite Automaton

Encoding Array d#

⭐ Convert the pattern string into a kind of encoding, and after conversion, the matching problem has nothing to do with the pattern string

Starting from position 0, read each position of the pattern string $t$ sequentially
When the character 'a' appears at position 0, set the element at index 'a' in the $d$ array to 1
When the character 'e' appears at position 1, set the element at index 'e' in the $d$ array to 1
And so on, obtaining the $d$ array
[PS]
- The index of the $d$ array can correspond to the ASCII code of the character
- The elements of the $d$ array can store int type [32 bits], long long type, or custom types, which determines the maximum length of the pattern string that can be matched
- Note the order of characters in the string and the numerical order of the $d$ array elements, the character at position 0 corresponds to the lower bits of the latter

State Information p#

Understand the state definition and feel the transition of states

State Definition: $p_i$
- In the binary representation of $p_i$, if the $j$-th bit is 1, it indicates that when ending with the text string $s[i]$, the first $j$ positions of the pattern string can be successfully matched
- Diagram, compare the above definition with the three pairs of circles below
  - Red: $p_4$ represents the current matching condition ending with the text string $s[4]$
  - Orange: The second bit of $p_4$ is 1, indicating that the first 2 positions of the pattern string $t$ can satisfy the above matching condition, i.e., $t[0\to 1]$ matches $s[3\to 4]$
  - Green: The fifth bit of $p_4$ is 1, indicating that the first 5 positions of the pattern string $t$ can satisfy the above matching condition, i.e., $t[0\to 4]$ matches $s[0\to 4]$
  - [PS]
    - The binary length of $p$ depends on what data type is used, like the elements of the $d$ array, such as int: 32 bits
    - Do not focus on how $p_4$ is obtained for now, we will look at the transition process later
- ⭐ It can be seen that
  - $p$ simultaneously stores information about multiple matching results❗
  - When the $n$-th bit of $p_i$ is 1, it indicates a successful match, that is
    - $p_i\ &\ (1\ <<\ (n-1))=1$
    - The matching position is: $i-n+1$
Transition Process: $p_i=(p_{i-1}\ <<\ 1\ |\ 1)\ &\ d[s[i]]$
- ⭐ Key Formula ⭐
- At this point, the pattern string $t$ has been completely abandoned, and through the previous state of $p$ and the $d$ array, the current value of $p$ can be obtained
- Principle analysis, compare the key formula with the diagram below ①②
  - Assuming $p_3$ is known, currently matching $s[2\to 3]$ and $s[0\to 3]$
  - ① Left shift by 1 + or 1 operation, obtain the transition state $p_4^{'}$
    - Left shift by 1: Attempting to swallow $s[4]$ based on the previous match, i.e., matching $s[2\to 4]$ and $s[0\to 4]$
      - The condition for successful matching lies in the subsequent and operation
      - [Note] The left shift operation appears as a right shift in the diagram because the order of digits is low on the left
    - Or 1 operation: Leave a chance for a separate match of $s[4]$, matching success indicates matching this one character
  - ② And operation
    - The above two operations are just attempts to match, and whether it is truly successful depends on the performance of $d[s_4]$
    - If the result of the and operation at the $j$-th bit is 1, it indicates a successful match of $s[4-j+1\to 4]$ with $t[0\to j-1]$
      - For example, if $p_4[2]=1$, $p_4[5]=1$, the matching result is as illustrated in the state definition part
[PS]
- The initial value of $p$ is 0, and $p$ is actually a non-deterministic finite state automaton
- Habitual conflict: Generally, the right side of the number order is the lower bit, but in the diagram, the left side of $p$ is the lower bit; the lowest bit of the binary number is 1, while the lowest bit of the string is 0; the elements of the $d$ array are numbers, so they should correspond to the numerical order, but the above diagram is to reflect the corresponding position relationship with the pattern string, using string order
- Accurately understand the meaning of $p$: The last successful match was 4 bits, and the next time it may successfully match 5 bits
- For matching problems with more than 64 bits, you need to create your own data type
  - Just support left shift, or, and operations
  - Then modify the types of the encoding array $d$ and state information $p$ accordingly

Summary#

① Encoding Array $d$: Converts the position of each character in the pattern string into the corresponding binary encoding
② State Information $p$: Transitions states through the key formula $p_i=(p_{i-1}\ <<\ 1\ |\ 1)\ &\ d[s[i]]$
Time Complexity: $O(m)$
- Completely does not require back and forth on the pattern string
- However, strictly speaking, it is not purely $O(m)$, which is related to the computer's data representation capability
❗ Can solve regular expression matching problems
- For example: $(a|b|c)&(c|d)&e&(f|a|b)$
- ① Convert the above pattern string into the encoding array $d$
  - For each column of the $d$ array, multiple bits can be set to 1
  - That is, each position of the pattern string can set multiple corresponding binary bits of the $d$ array elements to 1
- ② After that, it has nothing to do with the pattern string, solve the problem based on the $d$ array and the key formula
- [PS] Here it can be seen that the reason why the pattern string is called a pattern string is that it refers not only to strings but also to regular expressions (which can also be seen as a kind of related multi-pattern)

Code Demonstration#

Brute Force Matching Method#

Two versions, learn the skills of the concise version, flexibly use $flag$
Traverse the text string and the pattern string respectively, compare each position, if mismatched, move the text string pointer one position to the right
This idea is the foundation of all string matching algorithms

KMP#

2 programming methods, the latter is closer to the essence of the algorithm

① Ordinary coding: Directly obtain the $next$ array, then use the $next$ array for mismatch offset
- Preprocess the $next$ array → Traverse each position of the text string → Match the pattern string [using the $next$ array]
- ❗ Observe: The process of obtaining the $next$ array is very similar to the process of matching the text string, based on the state machine idea, the two parts can be integrated
② Advanced programming: Based on the state machine idea, transform the process of obtaining the $next$ value into a state change process
- Abstracted a state machine model: $j$ points to the position of the state machine, the $getNext$ method is equivalent to performing a state transition based on the input character, which is actually changing the value of $j$
- A way of thinking that is closer to the essence of KMP
PS: The $next$ array should also be freed before returning $i-n+1$ when matching is successful

SUNDAY#

❗ Note the meaning of 256: Used to record the position of each character in the pattern string
The process of preprocessing the $offset$ array: First initialize to all not appearing, $n+1$ indicates that the text string pointer can directly move right by a distance of the length of the pattern string + 1; during preprocessing, the positions of the same characters appearing later will overwrite those before, which is exactly what SUNDAY intends
$s[i + n]$: The character corresponding to the golden alignment point
$i + n <= m$: Reasonably utilizes the $n$, $m$ variables, indicating that the text string is still sufficient for the pattern string to match
Compared to KMP, SUNDAY is easier to understand, and the code is easier to implement [the best choice for solving simple single-pattern matching problems]

SHIFT-AND#

⭐ Beautiful idea, simple code
Note
- The $d$ array elements related to numbers and state $p$, the lowest bit is 1; while the string corresponds to 0
- But the transition process is arithmetic between numbers, so there is no need to worry about whether the positions are aligned

In-Class Exercises#

——Hash——#

Common problem-solving routine

HZOJ-275: Rabbits and Rabbits#

Sample Input

aabbaabb
3
1 3 5 7
1 3 6 8
1 2 1 2

Sample Output

Yes
No
Yes

Idea
- Note: The number of queries is particularly large, and the query interval is very large, brute force matching will definitely time out
- How to compare quickly? 👉 Hash matching algorithm
  - By hashing, represent the string with numbers <hash value>
  - If the hash values of the two strings are different, the two strings must not be equal
    - This eliminates most of the unequal cases without needing to compare bit by bit
  - Otherwise, verify whether the strings are equal through brute force matching
    - If the two strings are equal, one match can succeed
  - [PS]
    - The hash value corresponding to long strings may be too large, so generally, the hash value is reduced through modulus operation
    - If the remainders are different 👉 the strings must be different
- Design a hash function [string -> hash value]
  - $H=(\sum_{k=0}^{n-1}{C_k\times base^k})%P$
  - $n$: Length of the string $s$
  - $C_k$: ASCII code value corresponding to the $k$-th character
  - $base$: Weight [prime number]
  - $P$: Modulus [prime number]
  - [PS] Characters are stored in binary numbers at the computer's lower level
- ⭐ The hash value $H_{j\to i}$ of a substring $s[j\to i]$ in this problem
  - Based on the relationship between strings and hash values, a prefix sum array based on hash can be preprocessed
    - $HS_i=(\sum_{k=0}^{i}{C_k\times base^k})%P$
  - Thus, the hash value based on hash for the substring $s[j\to i]$ is
    - $HS_{j\to i}=(\sum_{k=j}^{i}{C_k\times base^k})%P$
  - However, for the hash value of the substring, it should not include the positional information $j$, $i$ of the substring in the string, that is, the multiplier factor should start from $base^0$
  - Therefore, the interval sum $HS_{j\to i}$ should be divided by $base^j$, but for the modulus operation, division cannot be done directly, and the inverse element must be used
  - Finally, the hash value of the substring $s[j\to i]$ is converted to
    - $H_{j\to i}=HS_{j\to i}\times(base^j)^{-1}%P=(HS_i-HS_{j-1})\times(base^j)^{-1}%P$
    - $(base^j)^{-1}$: The inverse element of $base^j$
    - For the quick calculation of the inverse element, please refer to: Quickly find [mod] inverse element
- Solution Method ①
  - 1. Preprocess the prefix sum based on hash for each position in the text string, convenient for later interval sum calculation
  - 1. Use the interval sum and inverse element to obtain the hash value of a substring $s[i\to j]$:
    - $H_{j\to i}=HS_{j\to i}\times(base^j)^{-1}%P$
  - 1. Compare the hash values of the two substrings
    - If not equal, the substrings must be different
    - Otherwise, verify whether they are the same through brute force matching
  - ❗ The probability of two substrings being different but having the same hash value is $1/P$
- Solution Method ②
  - Based on Method ①, design two hash functions with different $P$ and $base$
  - Compare the two hash values corresponding to the two substrings
    - If both are equal, consider the two substrings the same
    - Otherwise, they must be different
  - ❗ The probability of two substrings being different but having the same hash value is $1/(P_1\times P_2)$
    - The error probability is extremely low, in fact, many algorithms are probabilistic algorithms
Code
- Method ①: Hash matching + brute force matching
- ① The $P$ value must be a prime number, otherwise some inverse elements are meaningless, leading to incorrect hash values
  - This can cause the same substring to correspond to different hash values
  - The sufficient and necessary condition for the existence of the inverse element: coprime
- ② Need to use long long type, as the values in the intermediate process may be very large
  - This increases the probability of different substrings corresponding to the same hash value, increasing the time cost [brute force matching]
- [PS]
  - Always remember to take modulus to prevent numbers from exceeding the representation range, even for long long
  - Ensure that the hash value is positive
    - The hash prefix sum array $H$ is not monotonically increasing because there are modulus operations during summation
  - A small $P$ value may lead to timeouts due to excessive brute force matching
- Method ②: Hash matching * 2
- Note: The two inverse element arrays should be initialized separately to ensure complete initialization [the range of traversal is different]
  - Or use the same $P$ and different $base$, which can be initialized together
- [PS] To be safe, you can also add brute force matching verification

Quickly Find [mod] Inverse Element#

⭐Derivation Process

Goal: Solve for $x\times x^{-1}\equiv1\ (mod\ P)$ in which $x^{-1}$
- [PS] Only consider the case where $x<P$, because all $x$ greater than $P$ can be converted to less than $P$ by taking modulus
Let: $P\ %\ x=r,P\ /\ x=k$
Then:
- $\begin{aligned}P&=kx+r\kx+r&\equiv0\ (mod\ P)\kx(x^{-1}r^{-1})+r(x^{-1}r^{-1})&\equiv0\ (mod\ P)\kr^{-1}+x^{-1}&\equiv0\ (mod\ P)\x^{-1}&\equiv-kr^{-1}\ (mod\ P)\\end{aligned}$
Ultimately, the problem of finding $x^{-1}$ is transformed into finding $r^{-1}$
- And $r$ is the remainder of the modulus $x$, so $r$ must be smaller than $x$
A large-scale problem 👉 A smaller-scale problem [recursion]
To ensure the inverse element is positive, one more processing step is needed
- $x^{-1}_{+}=(-kr^{-1}\ %\ P+P)\ %\ P$
[PS]
- Modular inverse: The sufficient and necessary condition for the existence of the inverse element is that $p$ and $x$ are coprime
- There are many methods to find the inverse element, refer to Inverse Element Knowledge Popularization (Beginner's Edition) — cnblogs

Code

Regardless of the modulus, the inverse of 1 is 1 [initialization]
Output results
- You can verify: The original number multiplied by the inverse element modulo is 1

Additional Knowledge Points#

The essential ideas of KMP and SHIFT-AND: State machine
The SUNDAY algorithm is commonly used in life, and the Hash matching algorithm is often used in problem-solving
DFA and NFA are knowledge from compiler theory
- Main difference: DFA is faster, NFA consumes less memory
- Refer to Difference between DFA and NFA — Stechies

Tips#

Before starting C++, make sure to finish the prerequisite courses
Becoming an expert in the field of algorithms relies on improving your aesthetic ability
Getting angry is a sign of incompetence, focus on doing the right thing! Step by step improvement, without seeking instant success