《C++程式設計》小作業

默認基於 C++11 標準

0228#

在 C++ 中實現複數類#

要求：
（1）保證數據的安全性
（2）通過構造函數直接給實部和虛部賦值
（3）完成複數的加減乘除運算

分析需求#

(1)：需將所有數據定義為 private 類型

(2)：可使用初始化列表

(3)：注意除法細節

代碼實現#

熟悉初始化列表、類內重載、運算符重載、友元函數等操作
除法運算細節
- 分母有理化 [分子的複數相乘可以利用已實現的複數乘法運算]
- 除法可能產生小數，所以類內的數據類型直接使用 double 型
整合測試用例，簡化測試流程
[PS] 友好輸出複數的邏輯，不夠美觀，不知道還有沒有更好的方式判斷正負

測試結果#

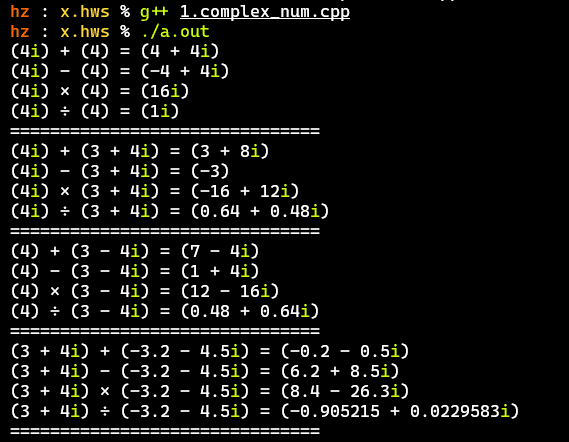
主要測試實數、純虛數、整數複數、小數複數之間的運算
計算結果無誤，基本符合上述需求

0227#

nth_element 函數的用法及技巧#

用法#

頭文件：<algorithm>

🔺 void nth_element

(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last);

功能：範圍內的某元素正確排序
- 重新排列 $[first, last)$ 範圍內的元素，讓nth位置的元素正好為升序排序後下標為nth的元素
參數列表
- first、last：待處理序列的起始、終止位置的隨機存取迭代器RandomAccessIterator [不包含終止位置的元素]
- nth：想要正確排序的隨機存取迭代器RandomAccessIterator
PS
- 所有指針都是有效的RandomAccessIterator
- 正確排序：其位置下標與其大小排序相同
- 其他元素沒有特定的順序，不過，在 $[first, last)$ 範圍內，nth元素左邊的元素都 $\le$ 它，右邊的元素都 $\ge$ 它

🔺 void nth_element

(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last, Compare comp);

增加參數comp：用於自定義排序規則
- bool cmp(const Type1 &a, const Type2 &b);
- 從 C++11 起，不允許使用Type1 &和Type1
- ❗ 定義小於規則，對應從小到大排序
- 傳入該參數時，既可以是函數指針，又可以是函數對象

技巧#

當不需要所有元素有序，而只需要取出位於某個排序位置的元素時，使用該方法更節省時間
平均時間複雜度：$O (N)$
基於快速選擇算法—— 知乎：借鑒快速排序的 Partition 過程，但不會對整個序列排序

⭕ 參考std::nth_element——cplusplus

string 的幾種基本操作的使用#

包括 find /insert/substr 函數及額外的三種方法
string 是一個 class；頭文件：<string>

find#

🔺 size_t find (const string& str, size_t pos = 0) const;

功能：在字符串中查找
- 從調用該方法的字符串的pos位置開始，查找並返回該字符串中第一次出現字符串str的位置下標
參數列表
- str：待查找的字符串
- pos：查找的起始位置；默認為0，查找整個被查找字符串
返回值：如果沒有找到，則返回string::npos
PS
- 類似的，可查找char *、char類型
- rfind()方法則從後往前找，pos默認為npos

insert#

🔺 string& insert (size_t pos, const string& str);

功能：在字符串中插入
- 在調用該方法的字符串的pos位置前，插入額外的字符串str
參數列表
- pos：要插入的位置，從0開始
- str：待插入的字符串
返回值：被插入字符串的自身引用，所以是在原地進行的該操作
PS：插入的是字符串的拷貝

substr#

🔺 string substr (size_t pos = 0, size_t len = npos) const;

功能：生成子串
- 返回調用該方法的字符串的子串的一個拷貝，該子串從pos位置開始，取len長度 [或者直到字符串的結尾]
參數列表
- pos：要被複製的子串的第一個字符的位置
- len：要複製的子串長度 [注意原字符串的長度]
PS：len默認指向npos，代表子串直接取到字符串的結尾

replace#

🔺 string& replace (size_t pos, size_t len, const string& str);

功能：替換字符串的某部分
- 使用字符串str替換調用該方法的字符串的某部分，該部分從pos位置開始，取len長度
參數列表
- pos：原字符串被替換的第一個字符位置
- len：被替換的部分長度 [同substr，注意原字符串的長度]
- str：待替換的字符串
返回值：原字符串本身
PS：替換前會拷貝 str

size#

🔺 size_t size() const noexcept;

功能：返回字符串的長度 [單位：字節]
PS
- 不計算末尾空字符'\0'
- 與length()方法同義

c_str#

🔺 const char* c_str() const noexcept;

功能：獲得等價的 C 形式字符數組
- 返回一個等價的字符數組指針，並且在數組結尾包含了空字符'\0'
PS：在 C++11 中，與data()方法同義

at#

🔺 char& at (size_t pos); const char& at (size_t pos) const;

功能：返回字符串pos位置對應的字符引用
參數pos：要獲取的字符的索引值，從0開始
PS：相比下標操作符[]，該方法在使用時
- 會檢查下標是否有效，無效時會拋出out_of_range異常
- 末尾'\0'字符的位置為無效的

⭕ 參考std::string——cplusplus

HZOJ-287 合併果子和 Huffman 編碼的關係#

Haffman 編碼過程#

先統計得到每一種字符的概率 $p_i\ |\ 1\le i\le n$
將 $n$ 個字符建立成一棵 Huffman 樹
- 每次拿出概率最小的兩個字符作為結點 $p_{min1}$ 、$p_{min2}$，合併，形成一個新的結點 $p_j$ [ $=p_{min1}+p_{min2}$ ]
- 再在剩余的結點中繼續上一步驟，合併 $n-1$ 次後，只剩下一個結點即完成建樹
按照某種形式 [如左分支 0、右分支 1] 將編碼讀取出來，得到每個字符對應的編碼 $code_i$

⭐ 又因為 Huffman 編碼是最優的變長編碼，即平均編碼長度 $\sum_{i=1}^n (len (code_i)\times p_i)$ 最小

[PS] $len (code_i)$ 表示編碼 $code_i$ 的長度

HZOJ-287 #

根據題目描述，求解步驟應為：

已知每堆果子的重量 $w_i\ |\ 1\le i\le n$ [等同需消耗的體力]
將 $n$ 堆果子按上述規則兩兩合併
- 需要理解的是，第 $i$ 堆果子可能被重複合併多次
- 假設第 $i$ 堆果子共進行了 $time_i$ 次合併，則總共消耗的體力為 $\sum_{i=1}^n (time_i\times w_i)$

⭐ 而題目要求總共消耗的體力最少，即 $\sum_{i=1}^n (time_i\times w_i)$ 最小

再觀察#

【兩者的優化對象】

Huffman 編碼 —— 平均編碼長度：$\sum_{i=1}^n (len (code_i)\times p_i)$
HZOJ-287—— 總共消耗的體力：$\sum_{i=1}^n (time_i\times w_i)$

❗ 將 $time_i$ 對應 $len (code_i)$，$w_i$ 對應 $p_i$，兩個公式完全一致

而Huffman 編碼可以使其優化對象達到最小，同理，可以使用 Huffman 編碼思想讓HZOJ-287的優化對象最小

👉 $w_i$ 越大的果子堆，被合併的次序應該越晚，即讓對應的 $time_i$ 儘可能小

👉👉 合併原則：每次拿出重量最小的兩個果子堆 $w_{min1}$ 、$w_{min2}$ 進行合併

綜上所述，HZOJ-287 合併果子的過程就是一個 Huffman 編碼的過程！