默认基于 C++11 标准
0228#
在 C++ 中实现复数类#
要求:
(1)保证数据的安全性
(2)通过构造函数直接给实部和虚部赋值
(3)完成复数的加减乘除运算
分析需求#
(1):需将所有数据定义为 private 类型
(2):可使用初始化列表
(3):注意除法细节
代码实现#



- 熟悉初始化列表、类内重载、运算符重载、友元函数等操作
- 除法运算细节
- 分母有理化 [分子的复数相乘可以利用已实现的复数乘法运算]
- 除法可能产生小数,所以类内的数据类型直接使用 double 型
- 整合测试用例,简化测试流程
- [PS] 友好输出复数的逻辑,不够美观,不知道还有没有更好的方式判断正负
测试结果#
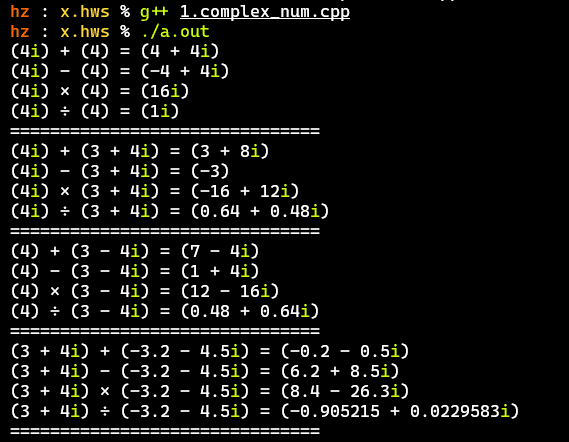
- 主要测试实数、纯虚数、整数复数、小数复数之间的运算
- 计算结果无误,基本符合上述需求
0227#
nth_element 函数的用法及技巧#
用法#
头文件:<algorithm>
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last);
- 功能:范围内的某元素正确排序
- 重新排列 $[first, last)$ 范围内的元素,让
nth位置的元素正好为升序排序后下标为nth的元素
- 重新排列 $[first, last)$ 范围内的元素,让
- 参数列表
first、last:待处理序列的起始、终止位置的随机存取迭代器RandomAccessIterator[不包含终止位置的元素]nth:想要正确排序的随机存取迭代器RandomAccessIterator
- PS
- 所有指针都是有效的
RandomAccessIterator - 正确排序:其位置下标与其大小排序相同
- 其他元素没有特定的顺序,不过,在 $[first, last)$ 范围内,
nth元素左边的元素都 $\le$ 它,右边的元素都 $\ge$ 它
- 所有指针都是有效的
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, andomAccessIterator last, Compare comp);
- 增加参数
comp:用于自定义排序规则bool cmp(const Type1 &a, const Type2 &b);- 从 C++11 起,不允许使用
Type1 &和Type1 - ❗ 定义小于规则,对应从小到大排序
- 传入该参数时,既可以是函数指针,又可以是函数对象
技巧#
-
当不需要所有元素有序,而只需要取出位于某个排序位置的元素时,使用该方法更节省时间
-
平均时间复杂度:$O (N)$
-
基于快速选择算法—— 知乎:借鉴快速排序的 Partition 过程,但不会对整个序列排序
⭕ 参考std::nth_element——cplusplus
string 的几种基本操作的使用#
包括 find /insert/substr 函数及额外的三种方法
string 是一个 class;头文件:<string>
find#
🔺 size_t find (const string& str, size_t pos = 0) const;
- 功能:在字符串中查找
- 从调用该方法的字符串的
pos位置开始,查找并返回该字符串中第一次出现字符串str的位置下标
- 从调用该方法的字符串的
- 参数列表
str:待查找的字符串pos:查找的起始位置;默认为0,查找整个被查找字符串
- 返回值:如果没有找到,则返回
string::npos - PS
- 类似的,可查找
char *、char类型 rfind()方法则从后往前找,pos默认为npos
- 类似的,可查找
insert#
🔺 string& insert (size_t pos, const string& str);
- 功能:在字符串中插入
- 在调用该方法的字符串的
pos位置前,插入额外的字符串str
- 在调用该方法的字符串的
- 参数列表
pos:要插入的位置,从0开始str:待插入的字符串
- 返回值:被插入字符串的自身引用,所以是在原地进行的该操作
- PS:插入的是字符串的拷贝
substr#
🔺 string substr (size_t pos = 0, size_t len = npos) const;
- 功能:生成子串
- 返回调用该方法的字符串的子串的一个拷贝,该子串从
pos位置开始,取len长度 [或者直到字符串的结尾]
- 返回调用该方法的字符串的子串的一个拷贝,该子串从
- 参数列表
pos:要被复制的子串的第一个字符的位置len:要复制的子串长度 [注意原字符串的长度]
- PS:
len默认指向npos,代表子串直接取到字符串的结尾
replace#
🔺 string& replace (size_t pos, size_t len, const string& str);
- 功能:替换字符串的某部分
- 使用字符串
str替换调用该方法的字符串的某部分,该部分从pos位置开始,取len长度
- 使用字符串
- 参数列表
pos:原字符串被替换的第一个字符位置len:被替换的部分长度 [同substr,注意原字符串的长度]str:待替换的字符串
- 返回值:原字符串本身
- PS:替换前会拷贝
str
size#
🔺 size_t size() const noexcept;
- 功能:返回字符串的长度 [单位:字节]
- PS
- 不计算末尾空字符
'\0' - 与
length()方法同义
- 不计算末尾空字符
c_str#
🔺 const char* c_str() const noexcept;
- 功能:获得等价的 C 形式字符数组
- 返回一个等价的字符数组指针,并且在数组结尾包含了空字符
'\0'
- 返回一个等价的字符数组指针,并且在数组结尾包含了空字符
- PS:在 C++11 中,与
data()方法同义
at#
🔺 char& at (size_t pos); const char& at (size_t pos) const;
- 功能:返回字符串
pos位置对应的字符引用 - 参数
pos:要获取的字符的索引值,从0开始 - PS:相比下标操作符
[],该方法在使用时- 会检查下标是否有效,无效时会抛出
out_of_range异常 - 末尾
'\0'字符的位置为无效的
- 会检查下标是否有效,无效时会抛出
⭕ 参考std::string——cplusplus
HZOJ-287 合并果子和 Huffman 编码的关系#
Haffman 编码过程#
- 先统计得到每一种字符的概率 $p_i\ |\ 1\le i\le n$
- 将 $n$ 个字符建立成一棵 Huffman 树
- 每次拿出概率最小的两个字符作为结点 $p_{min1}$ 、$p_{min2}$,合并,形成一个新的结点 $p_j$ [ $=p_{min1}+p_{min2}$ ]
- 再在剩余的结点中继续上一步骤,合并 $n-1$ 次后,只剩下一个结点即完成建树
- 按照某种形式 [如左分支 0、右分支 1] 将编码读取出来,得到每个字符对应的编码 $code_i$
⭐ 又因为 Huffman 编码是最优的变长编码,即平均编码长度 $\sum_{i=1}^n (len (code_i)\times p_i)$ 最小
[PS] $len (code_i)$ 表示编码 $code_i$ 的长度
HZOJ-287#

根据题目描述,求解步骤应为:
- 已知每堆果子的重量 $w_i\ |\ 1\le i\le n$ [等同需消耗的体力]
- 将 $n$ 堆果子按上述规则两两合并
- 需要理解的是,第 $i$ 堆果子可能被重复合并多次
- 假设第 $i$ 堆果子共进行了 $time_i$ 次合并,则总共消耗的体力为 $\sum_{i=1}^n (time_i\times w_i)$
⭐ 而题目要求总共消耗的体力最少,即 $\sum_{i=1}^n (time_i\times w_i)$ 最小
再观察#
【两者的优化对象】
-
Huffman 编码 —— 平均编码长度:$\sum_{i=1}^n (len (code_i)\times p_i)$
-
HZOJ-287—— 总共消耗的体力:$\sum_{i=1}^n (time_i\times w_i)$
❗ 将 $time_i$ 对应 $len (code_i)$,$w_i$ 对应 $p_i$,两个公式完全一致
而Huffman 编码可以使其优化对象达到最小,同理,可以使用 Huffman 编码思想让HZOJ-287的优化对象最小
👉 $w_i$ 越大的果子堆,被合并的次序应该越晚,即让对应的 $time_i$ 尽可能小
👉👉 合并原则:每次拿出重量最小的两个果子堆 $w_{min1}$ 、$w_{min2}$ 进行合并
综上所述,HZOJ-287 合并果子的过程就是一个 Huffman 编码的过程!