デフォルトは C++11 標準に基づく
0228#
C++ で複素数クラスを実装する#
要求:
(1)データの安全性を確保する
(2)コンストラクタを通じて実部と虚部に値を直接与える
(3)複素数の加減乗除演算を完了する
要件分析#
(1):すべてのデータを private 型として定義する必要がある
(2):初期化リストを使用できる
(3):除算の詳細に注意する
コード実装#



- 初期化リスト、クラス内オーバーロード、演算子オーバーロード、友元関数などの操作に慣れる
- 除算の詳細
- 分母の有理化 [分子の複素数を掛けることにより、実装済みの複素数乗法演算を利用できる]
- 除算は小数を生成する可能性があるため、クラス内のデータ型は直接 double 型を使用する
- テストケースを統合し、テストプロセスを簡素化する
- [PS] 複素数の友好的な出力ロジックは美しくなく、正負を判断するより良い方法があるかどうかわからない
テスト結果#
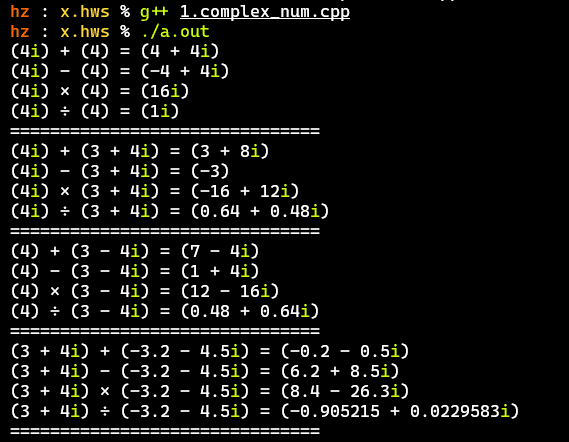
- 主に実数、純虚数、整数複素数、小数複素数間の演算をテストする
- 計算結果は正確で、基本的に上記の要件を満たしている
0227#
nth_element 関数の使い方とテクニック#
使い方#
ヘッダーファイル:<algorithm>
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last);
- 機能:範囲内の特定の要素を正しくソートする
- $[first, last)$ 範囲内の要素を再配置し、
nth位置の要素がちょうど昇順ソート後のインデックスnthの要素になるようにする
- $[first, last)$ 範囲内の要素を再配置し、
- パラメータリスト
first、last:処理対象のシーケンスの開始、終了位置のランダムアクセスイテレータRandomAccessIterator[終了位置の要素は含まない]nth:正しくソートされたランダムアクセスイテレータRandomAccessIterator
- PS
- すべてのポインタは有効な
RandomAccessIterator - 正しくソートされている:その位置インデックスとそのサイズのソートが同じ
- 他の要素には特定の順序はないが、$[first, last)$ 範囲内で、
nth要素の左側の要素はすべて $\le$ それであり、右側の要素はすべて $\ge$ それである
- すべてのポインタは有効な
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last, Compare comp);
- パラメータ
compを追加:カスタムソートルールに使用bool cmp(const Type1 &a, const Type2 &b);- C++11 以降、
Type1 &とType1の使用は許可されていない - ❗ 小さいルールを定義し、昇順にソートする
- このパラメータを渡すと、関数ポインタまたは関数オブジェクトのいずれかを使用できる
テクニック#
-
すべての要素が順序付けられる必要がなく、特定のソート位置にある要素を取得するだけでよい場合、この方法を使用すると時間を節約できる
-
平均時間計算量:$O (N)$
-
クイックセレクトアルゴリズムに基づく ——Zhihu:クイックソートのパーティションプロセスを参考にしているが、シーケンス全体をソートすることはない
⭕ 参考std::nth_element——cplusplus
string のいくつかの基本操作の使用#
find /insert/substr 関数および追加の 3 つの方法を含む
string はクラスです;ヘッダーファイル:<string>
find#
🔺 size_t find (const string& str, size_t pos = 0) const;
- 機能:文字列内を検索する
- このメソッドを呼び出した文字列の
pos位置から始めて、文字列strが最初に出現する位置のインデックスを検索して返す
- このメソッドを呼び出した文字列の
- パラメータリスト
str:検索対象の文字列pos:検索の開始位置;デフォルトは0で、検索対象の文字列全体を検索する
- 戻り値:見つからなかった場合は
string::nposを返す - PS
- 同様に、
char *、char型を検索できる rfind()メソッドは後ろから前に検索し、posのデフォルトはnpos
- 同様に、
insert#
🔺 string& insert (size_t pos, const string& str);
- 機能:文字列に挿入する
- このメソッドを呼び出した文字列の
pos位置の前に追加の文字列strを挿入する
- このメソッドを呼び出した文字列の
- パラメータリスト
pos:挿入位置、0から始まるstr:挿入する文字列
- 戻り値:挿入された文字列の自身の参照であり、原地でこの操作を行う
- PS:挿入されるのは文字列のコピーである
substr#
🔺 string substr (size_t pos = 0, size_t len = npos) const;
- 機能:サブストリングを生成する
- このメソッドを呼び出した文字列のサブストリングのコピーを返す。このサブストリングは
pos位置から始まり、lenの長さを取る [または文字列の末尾まで]
- このメソッドを呼び出した文字列のサブストリングのコピーを返す。このサブストリングは
- パラメータリスト
pos:コピーされるサブストリングの最初の文字の位置len:コピーされるサブストリングの長さ [元の文字列の長さに注意]
- PS:
lenはデフォルトでnposを指し、サブストリングは文字列の末尾まで取る
replace#
🔺 string& replace (size_t pos, size_t len, const string& str);
- 機能:文字列の一部を置き換える
- 文字列
strを使用して、このメソッドを呼び出した文字列の一部を置き換える。この部分はpos位置から始まり、lenの長さを取る
- 文字列
- パラメータリスト
pos:元の文字列が置き換えられる最初の文字の位置len:置き換えられる部分の長さ [substrと同様に、元の文字列の長さに注意]str:置き換える文字列
- 戻り値:元の文字列自体
- PS:置き換えの前に
strがコピーされる
size#
🔺 size_t size() const noexcept;
- 機能:文字列の長さを返す [単位:バイト]
- PS
- 終端の空文字
'\0'は計算しない length()メソッドと同義
- 終端の空文字
c_str#
🔺 const char* c_str() const noexcept;
- 機能:等価な C 形式の文字配列を取得する
- 等価な文字配列ポインタを返し、配列の末尾には空文字
'\0'が含まれている
- 等価な文字配列ポインタを返し、配列の末尾には空文字
- PS:C++11 では、
data()メソッドと同義
at#
🔺 char& at (size_t pos); const char& at (size_t pos) const;
- 機能:文字列
pos位置に対応する文字の参照を返す - パラメータ
pos:取得する文字のインデックス値、0から始まる - PS:インデックス操作子
[]と比較して、このメソッドを使用する際- インデックスが有効かどうかをチェックし、有効でない場合は
out_of_range例外をスローする - 末尾の
'\0'文字の位置は無効である
- インデックスが有効かどうかをチェックし、有効でない場合は
⭕ 参考std::string——cplusplus
HZOJ-287 果物の合併と Huffman 符号化の関係#
Huffman 符号化プロセス#
- まず、各文字の確率 $p_i\ |\ 1\le i\le n$ を統計する
- $n$ 個の文字を Huffman 木に構築する
- 確率が最小の 2 つの文字をノード $p_{min1}$ 、$p_{min2}$ として取り出し、合併して新しいノード $p_j$ を形成する [ $=p_{min1}+p_{min2}$ ]
- 残りのノードの中でこの手順を続け、合併を $n-1$ 回行った後、1 つのノードが残ると木の構築が完了する
- ある形式 [例えば左分岐 0、右分岐 1] に従って符号を読み取り、各文字に対応する符号 $code_i$ を得る
⭐ さらに Huffman 符号化は最適な可変長符号であり、すなわち平均符号長 $\sum_{i=1}^n (len (code_i)\times p_i)$ が最小である
[PS] $len (code_i)$ は符号 $code_i$ の長さを示す
HZOJ-287#

問題の説明に基づいて、解決手順は次のようになる:
- 各果物の山の重量 $w_i\ |\ 1\le i\le n$ [消費する体力に等しい]
- 上記のルールに従って、$n$ 山の果物を 2 つずつ合併する
- 理解すべきことは、第 $i$ 山の果物が複数回合併される可能性があること
- 第 $i$ 山の果物が合併された回数を $time_i$ と仮定すると、消費される体力の合計は $\sum_{i=1}^n (time_i\times w_i)$ である
⭐ そして問題は、消費される体力の合計が最小であること、すなわち $\sum_{i=1}^n (time_i\times w_i)$ が最小であることを要求している
再観察#
【両者の最適化対象】
-
Huffman 符号化 —— 平均符号長:$\sum_{i=1}^n (len (code_i)\times p_i)$
-
HZOJ-287—— 消費される体力の合計:$\sum_{i=1}^n (time_i\times w_i)$
❗ $time_i$ を $len (code_i)$ に、$w_i$ を $p_i$ に対応させると、2 つの式は完全に一致する
そしてHuffman 符号化はその最適化対象を最小化できるため、同様にHZOJ-287の最適化対象を最小化するために Huffman 符号化の考え方を使用できる
👉 $w_i$ が大きい果物の山は、合併される順序が遅くなるべきであり、すなわち対応する $time_i$ をできるだけ小さくする
👉👉 合併の原則:毎回重量が最小の 2 つの果物の山 $w_{min1}$ 、$w_{min2}$ を取り出して合併する
以上から、HZOJ-287 果物の合併プロセスは Huffman 符号化のプロセスである!