Based on the C++11 standard by default
0228#
Implementing Complex Number Class in C++#
Requirements:
(1) Ensure the security of data
(2) Assign values to the real and imaginary parts directly through the constructor
(3) Perform addition, subtraction, multiplication, and division operations on complex numbers
Analyzing the Requirements#
(1): All data should be defined as private
(2): Initialization list can be used
(3): Pay attention to the details of division
Code Implementation#



- Familiarize yourself with initialization lists, overloaded functions within classes, operator overloading, and friend functions
- Pay attention to the details of division
- The denominator can be rationalized [Multiplying the numerator by the complex conjugate can utilize the already implemented complex multiplication operation]
- Division may result in decimals, so the data type within the class should be double
- Consolidate test cases to simplify the testing process
- [PS] The logic for friendly output of complex numbers is not very aesthetic. Not sure if there is a better way to determine the positive or negative sign
Test Results#
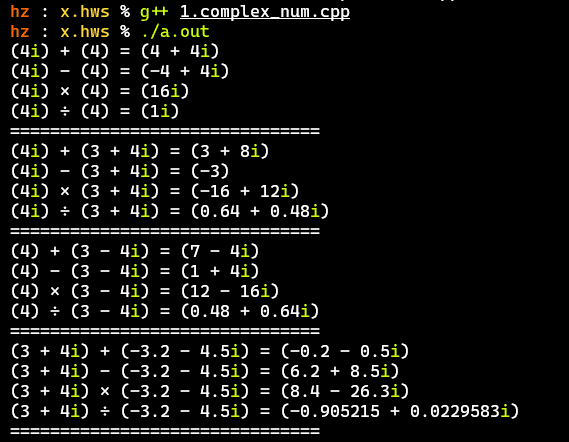
- Mainly tested the operations between real numbers, pure imaginary numbers, complex numbers with integers, and complex numbers with decimals
- The calculation results are correct and generally meet the above requirements
0227#
Usage and Tips for nth_element Function#
Usage#
Header file: <algorithm>
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, RandomAccessIterator last);
- Function: Correctly sort an element within a range
- Rearranges the elements in the range $[first, last)$ in such a way that the element at the
nthposition is the element that would be in that position in a sorted sequence
- Rearranges the elements in the range $[first, last)$ in such a way that the element at the
- Parameter List
first,last: Random-access iterators to the initial and final positions of the sequence to be sorted [excluding the element pointed bylast]nth: Random-access iterator to the element to be sorted correctly
- PS
- All pointers are valid random-access iterators
- Correct sorting: The position index of the element matches its sorted order
- The order of the other elements is not specified, but within the range $[first, last)$, all elements to the left of
nthare $\le$ it, and all elements to the right are $\ge$ it
🔺 void nth_element
(RandomAccessIterator first, RandomAccessIterator nth, andomAccessIterator last, Compare comp);
- Additional parameter
comp: Used to define a custom sorting rulebool cmp(const Type1 &a, const Type2 &b);- Starting from C++11,
Type1 &andType1are not allowed - ❗ Define the less-than rule for ascending order
- When passing this parameter, it can be either a function pointer or a function object
Tips#
- When you only need to retrieve the element at a certain sorted position and do not need all elements to be sorted, using this method can save time
- Average time complexity: $O(N)$
- Based on the Quickselect algorithm: Borrowing the partition process of quicksort, but not sorting the entire sequence
⭕ Reference: std::nth_element - cplusplus
Usage of Basic Operations of string#
Including the functions find / insert / substr and three additional methods
string is a class; Header file: <string>
find#
🔺 size_t find (const string& str, size_t pos = 0) const;
- Function: Find a substring in a string
- Searches the string for the first occurrence of the sequence specified by its arguments, starting from the position
posin the string
- Searches the string for the first occurrence of the sequence specified by its arguments, starting from the position
- Parameter List
str: The string to be searched forpos: The position to start the search from; defaults to0, which means the entire string is searched
- Return Value: If the substring is found, it returns the position of the first character of the first match. If the substring is not found, it returns
string::npos - PS
- Similar functions can be used to search for
char *andchartypes - The
rfind()function searches from the end to the beginning, withposdefaulting tonpos
- Similar functions can be used to search for
insert#
🔺 string& insert (size_t pos, const string& str);
- Function: Insert a string into another string
- Inserts additional characters into the string right before the character indicated by
pos
- Inserts additional characters into the string right before the character indicated by
- Parameter List
pos: The position where the insertion starts, counting from0str: The string to be inserted
- Return Value: A reference to the string itself, so the operation is performed in place
- PS: A copy of the string is inserted
substr#
🔺 string substr (size_t pos = 0, size_t len = npos) const;
- Function: Generate a substring
- Returns a newly constructed string object with its value initialized to a copy of a substring of this object
- Parameter List
pos: Position of the first character to be copied as a substringlen: Number of characters to include in the substring [or until the end of the string]
- PS:
lendefaults tonpos, which means the substring goes to the end of the string
replace#
🔺 string& replace (size_t pos, size_t len, const string& str);
- Function: Replace a portion of the string
- Replaces a portion of the string with a copy of
str
- Replaces a portion of the string with a copy of
- Parameter List
pos: Position of the first character to be replacedlen: Number of characters to replace [same assubstr, pay attention to the length of the original string]str: The string to replace with
- Return Value: The original string itself
- PS: The string is copied before the replacement is made
size#
🔺 size_t size() const noexcept;
- Function: Return the length of the string in bytes
- PS
- Does not count the null character
'\0' - Equivalent to the
length()method
- Does not count the null character
c_str#
🔺 const char* c_str() const noexcept;
- Function: Get a pointer to a null-terminated character array with data equivalent to those stored in the string
- PS: In C++11, equivalent to
data()
at#
🔺 char& at (size_t pos); const char& at (size_t pos) const;
- Function: Return a reference to the character at position
posin the string - Parameter
pos: The index of the character to retrieve, starting from0 - PS: Compared to the subscript operator
[], this method- Checks whether the index is valid and throws an
out_of_rangeexception if it is not - The position of the null character
'\0'is considered invalid
- Checks whether the index is valid and throws an
⭕ Reference: std::string - cplusplus
The Relationship Between Merging Fruits and Huffman Encoding in HZOJ-287#
Huffman Encoding Process#
- First, calculate the probability $p_i$ for each character
- Build a Huffman tree with the $n$ characters
- Take the two characters with the smallest probabilities as nodes $p_{min1}$ and $p_{min2}$, merge them to form a new node $p_j$ [ $=p_{min1}+p_{min2}$ ]
- Continue the previous step with the remaining nodes, merge $n-1$ times until there is only one node left, completing the tree
- Read the encoding in a certain form [e.g., left branch 0, right branch 1] to obtain the encoding $code_i$ for each character
⭐ Since Huffman encoding is an optimal variable-length encoding, the average encoding length $\sum_{i=1}^n(len(code_i)\times p_i)$ is minimized
[PS] $len(code_i)$ represents the length of the encoding $code_i$
HZOJ-287#

According to the problem description, the solution steps should be:
- Given the weight $w_i$ of each pile of fruits [equivalent to the physical strength required]
- Merge the $n$ piles of fruits according to the above rules
- It is important to understand that the $i$th pile of fruits may be merged multiple times
- Assuming the $i$th pile of fruits is merged $time_i$ times, the total physical strength consumed is $\sum_{i=1}^n(time_i\times w_i)$
⭐ The problem requires minimizing the total physical strength consumed, which is $\sum_{i=1}^n(time_i\times w_i)$
Further Observation#
【Optimization Objects】
-
Huffman Encoding - Average Encoding Length: $\sum_{i=1}^n(len(code_i)\times p_i)$
-
HZOJ-287 - Total Physical Strength Consumed: $\sum_{i=1}^n(time_i\times w_i)$
❗ Let $time_i$ correspond to $len(code_i)$, and $w_i$ correspond to $p_i$, the two formulas are exactly the same
Huffman encoding can minimize its optimization object. Similarly, we can use the Huffman encoding idea to minimize the optimization object of HZOJ-287
👉 The larger the weight $w_i$ of a pile of fruits, the later it should be merged, which means making the corresponding $time_i$ as small as possible
👉👉 Merging Principle: Take out the two piles of fruits with the smallest weights $w_{min1}$ and $w_{min2}$ for merging
In conclusion, the process of merging fruits in HZOJ-287 is the same as the process of Huffman encoding!